高三数学复习 1.1.2余弦定理课件VIP免费

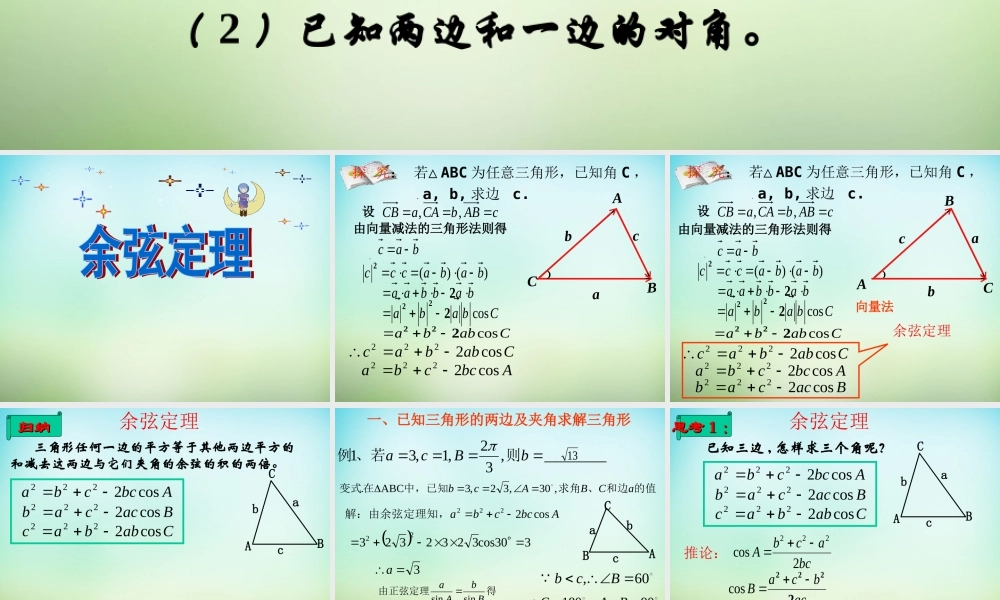
正弦定理：CcBbAasinsinsinR2可以解决两类有关三角形的问题 ?（ 1 ）已知两角和任一边。（ 2 ）已知两边和一边的对角。CRcBRbARasin2,sin2,sin2变型：BAbaBACBAcbasinsinsin:sin:sin::复习回顾复习回顾CBAcab﹚Abccbacos2222﹚ 探 究 △： 若ABC 为任意三角形，已知角 C ， a, b, 求边c.cABbCAaCB,,设)()(babaccc2babbaa2Cabbacos222Cabbaccos2222由向量减法的三角形法则得Cbabacos222bacCBAcab﹚Baccabcos2222余弦定理Abccbacos2222babbaa2Cabbacos222Cabbaccos2222由向量减法的三角形法则得Cbabacos222 探 究 △： 若ABC 为任意三角形，已知角 C ， a, b, 求边c.cABbCAaCB,,设bac向量法)()(babaccc2余弦定理 三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。Cabbaccos2222Abccbacos2222Baccabcos2222CBAbac归纳归纳一、已知三角形的两边及夹角求解三角形的值和边、求角中，已知在变式aCBAcb,30,32,3ABC.Abccbacos2222解：由余弦定理知，3a得由正弦定理BbAasinsin233213sinBsinaAb330cos323232322CABabc________,32,1,31bBca则、若例1360,Bcb90180CBA余弦定理 已知三边 , 怎样求三个角呢？Cabbaccos2222Abccbacos2222Baccabcos2222bcacbA2cos222acbcaB2222cosabcbaC2cos222推论：CBAbac思考思考 11 ：：__________,2,1,3.1BABACBCABC则中，若在三角形30120.13545.60.________,.2222DCBACabbcaABC或的大小为则角中，在三角形30C60212cos2cos222222CababCabbcaabcbaC解析：二、已知三角函数的三边解三角形_____,8,3,7.3ABCScbaABC则中，若在三角形36 由推论我们能判断三角形的角的情况吗 ?bcacbA2cos222推论：CBAbac思考思考 22 ：：提炼：设 a 是最长的边，则△ABC 是钝角三角形222acb△ABC 是锐角三角形222acb△ABC 是直角三角形222acb例 3 、在△ ABC 中，若 ， 则△ ABC 的形状为（ ）222cbaＡ、钝角三角形 Ｂ、...