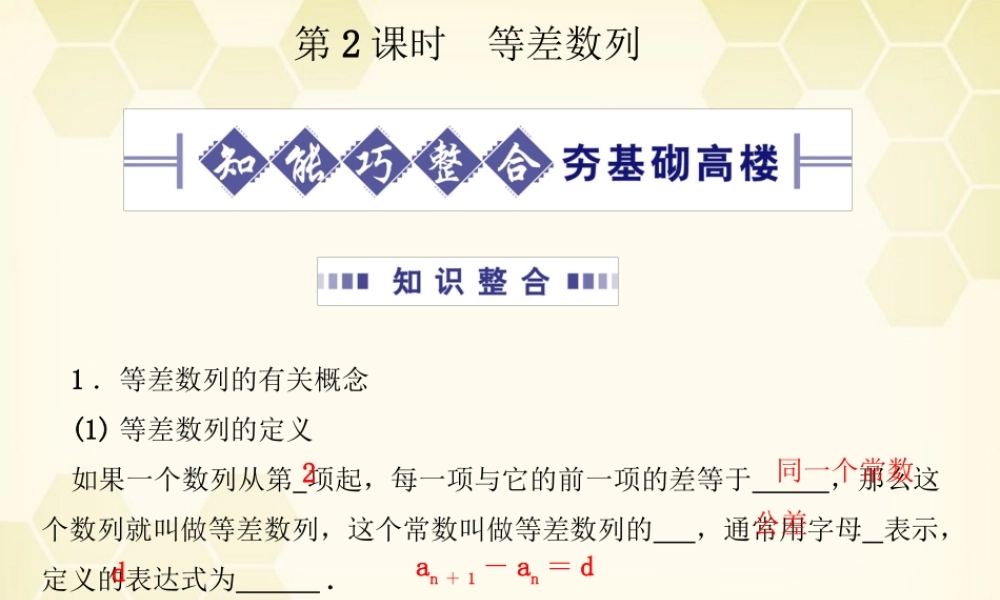
第 2 课时等差数列1 .等差数列的有关概念(1) 等差数列的定义如果一个数列从第 项起,每一项与它的前一项的差等于 ,那么这个数列就叫做等差数列,这个常数叫做等差数列的 ,通常用字母 表示,定义的表达式为 .2同一个常数公差dan + 1 - an = d2 .等差数列的性质已知数列 {an} 是等差数列, Sn 是其前 n 项和.(1) 若 m + n = p + q ,则 .特别:若 m + n = 2p ,则 am + an = 2ap.(2)am , am + k , am + 2k , am + 3k ,…仍是等差数列,公差为 .(3) 数列 Sm , S2m - Sm , S3m - S2m ,…也是等差数列.am + an = ap + aqkd1 . (2010· 重庆卷 ) 在等差数列 {an} 中, a1 + a9 = 10 ,则 a5 的值为( )A . 5 B . 6C . 8 D . 10解析: 在等差数列 {an} 中, 2a5 = a1 + a9 = 10 ,∴ a5 = 5.答案: A判断或证明数列 {an} 为等差数列的常见方法:(1) 利用定义: an + 1 - an = d( 常数 )(n∈N) ;(2) 利用等差中项: 2an + 1 = an + an + 2 ;(3) 利用通项公式: an = dn + c(d 、 c 为常数 ) , d 为公差.当d≠0 时,通项公式 an 是关于 n 的一次函数; d = 0 时为常函数,也是等差数列;(4) 利用前 n 项和公式: Sn = an2 + bn(a 、 b 为常数 ) .若一个数列的前 n 项和为关于 n 的二次函数且不含常数项,则这个数列为公差不等于零的等差数列;若此时的 a = 0 ,则此数列为常数列.2 .数列的通项公式和前 n 项和公式在解题中起到变量代换作用,而 a1 和 d 是等差数列的两个基本量,用它们表示已知和未知是常用方法.1 .等差数列的单调性等差数列公差为 d ,若 d > 0 ,则数列递增;若 d < 0 ,则数列递减;若 d = 0 ,则数列为常数列.2 .等差数列的最值若 {an} 是等差数列,求前 n 项和的最值时,(3) 除上面方法外,还可将 {an} 的前 n 项和的最值问题看作 Sn关于 n 的二次函数最值问题,利用二次函数的图象或配方法求解,注意 n∈N.已知数列 {an} 是等差数列.(1) 前四项和为 21 ,末四项和为 67 ,且前 n 项和为 286 ,求 n ;(2) 若 Sn = 20 , S2n = 38 ,求 S3n ;(3) 若项数为奇数,且奇数项和为 44 ,偶数项和...