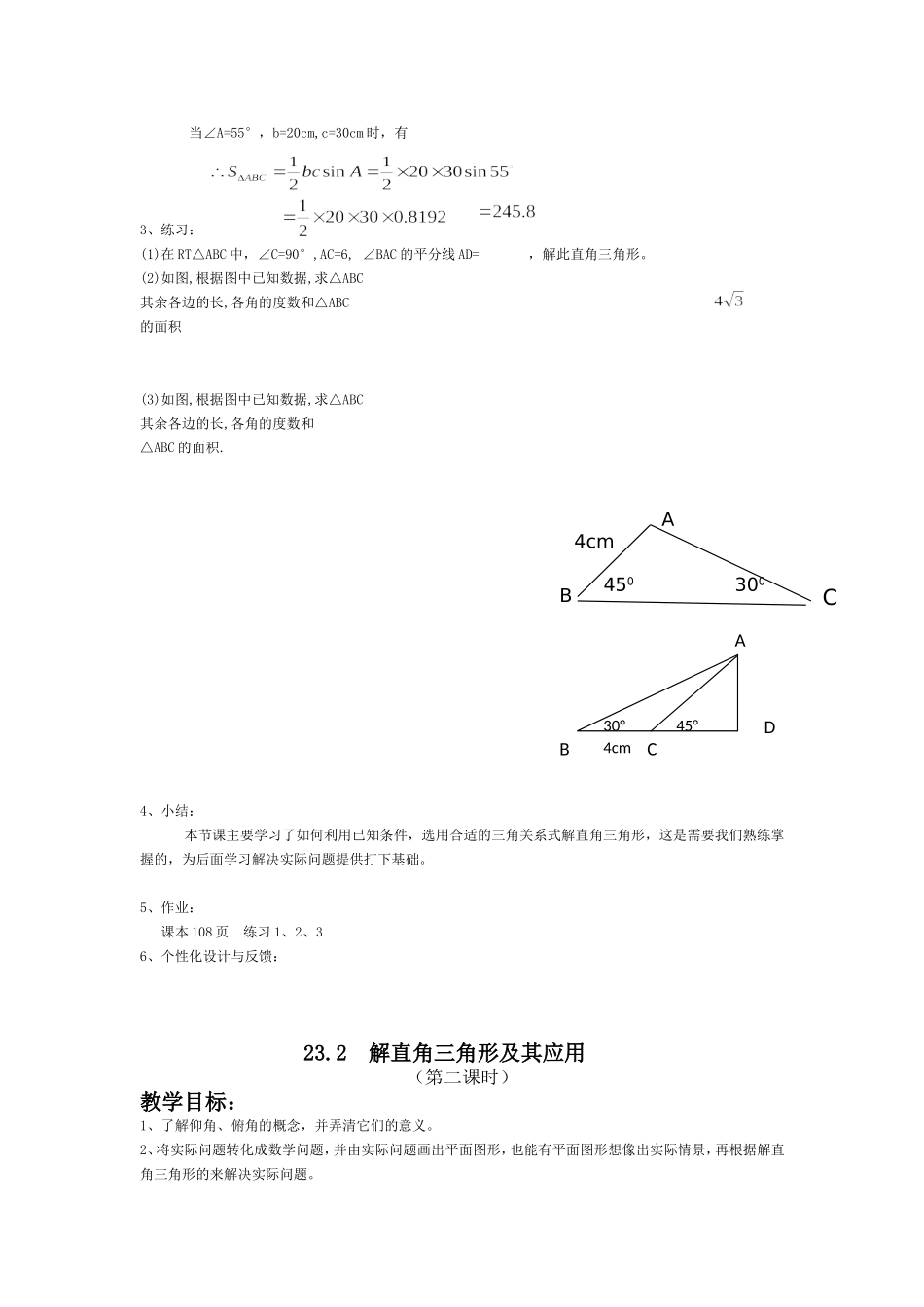
23.2 解直角三角形及其应用 (第一课时)教学目标:1、熟练掌握直角三角形除直角外五个元素之间的关系。2、学会根据题目要求正确地选用这些关系式解直角三角形。教学重难点:1、重点:会利用已知条件解直角三角形。2、难点:根据题目要求正确选用适当的三角关系式解直角三角形。教学过程:1、复习回顾*直角三角形三边的关系: 勾股定理 a2+b2=c2.直角三角形两锐角的关系:两锐角互余 ∠A+ ∠B=90°.*直角三角形边与角之间的关系:锐角三角函数*互余两角之间的三角函数关系: sinA=cosB.*同角之间的三角函数关系:*特殊角 30°,45°,60°角的三角函数值.2、新课探究:有以上的关系,如果知道了五个元素中的两个元素(至少有一个是边),就可以求出其余的三个元素。在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形。例 1 在 RT△ABC 中,∠C=90°,∠B=42°6′,c=287.4,解这个三角形。解:∠A=90°-42°6′=47°54′ a=c·cosB=287.4×0.7420=213.3 b=c·sinB=287.4×0.6704=192.7 例 2 在△ABC 中,∠A=55°,b=20cm,c=30cm,求三角形的面积 (精确到 0.1cm2)解:如图,作 AB 上的高 CD,在 RT△ACD 中,CD=AC·sinA=b·sinA.A C a c b BcaBAcossincbBAsincos当∠A=55°,b=20cm,c=30cm 时,有3、练习:(1)在 RT△ABC 中,∠C=90°,AC=6, ∠BAC 的平分线 AD= ,解此直角三角形。(2)如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积(3)如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC 的面积.4、小结:本节课主要学习了如何利用已知条件,选用合适的三角关系式解直角三角形,这是需要我们熟练掌握的,为后面学习解决实际问题提供打下基础。 5、作业: 课本 108 页 练习 1、2、3 6、个性化设计与反馈:23.2 解直角三角形及其应用(第二课时)教学目标:1、了解仰角、俯角的概念,并弄清它们的意义。2、将实际问题转化成数学问题,并由实际问题画出平面图形,也能有平面图形想像出实际情景,再根据解直角三角形的来解决实际问题。ABC4503004cmADCB30°45°4cm教学重难点:1、重点:将实际问题转化成数学问题且了解仰角、俯角的概念。2、难点:实际情景和平面图形之间的转化。教学过程:1、复习回顾:① 直角三角形三边的关系: 勾股定理 a2+b2=c2.直角三角形两锐角的关系:两锐角互余 ∠A+ ∠B=90°.*直角三角形边与角之间的关系:...