高考数学复习(空间向量的基本定理) 试题VIP免费

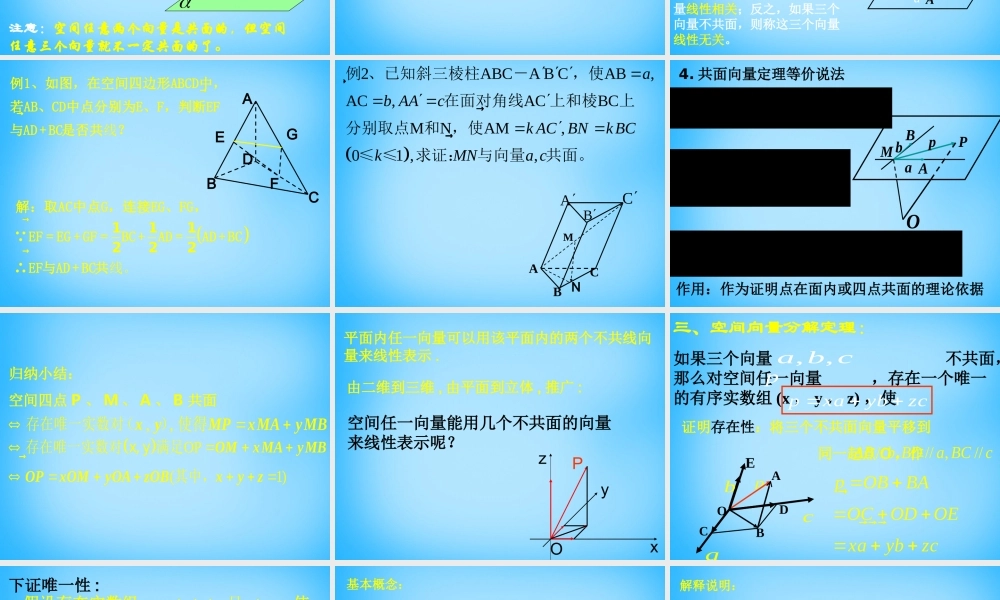
一、复习提问：1. 什么是空间共线向量？若空间向量的基线平行或重合，则这些向量叫做共线向量或平行向量。//ab记作注：零向量与任一向量是共线向量。2. 平行向量基本定理：, (0),//.a b babab对于平面内任意两个向量存在唯一实数 使作用：在平面内判定向量平行（共线）。3. 平面向量基本定理：2121 122,,,eeaa aaa ea e���1如果 和 是一平面内的两个不共线的向量，那么该平面内的任一向量存在唯一的一对实数使 ＝二：新授,0//.a b babxaxb两个空间向量 ，，则的充要条件是存在唯一的实数 ，使注： （ 1 ）此为充要条件； 0b x（ 2 ）定理中条件否则实数就不唯一。 是必须的，（ 3 ）共线向量且基线不重合时可证平行一、共线向量定理二 . 共面向量 :平行于同一平面的向量OAba注意：空间任意两个向量是共面的，但空间任意三个向量就不一定共面的了。1 、向量与平面平行 :,,OA//aOAaaaa��已知向量作如果 的基线平行于平面 或在平面 内，则称向量 平行于平面 ，记作2 、共面向量：3 、共面向量定理,a bc如果两个向量 不共线 , 则向量 与向量 共面的充要条件是存在唯一实数对 使如果两个向量 不共线 , 则向量 与向量 共面的充要条件是存在唯一实数对 使cxayb,a b,x y1xayb证明：如果向量c与向量a、b共面，可以通过平移，使它们位于同一平面内，由平面向量基本定理知：一定存在唯一的实数对x（）必要性c：, y使,(2),Oxa OByb��如果c满足关系式：c=xa+yb,则可选定一点 ，作OA于是OC=O充分性：A+AC=xa+yb=c，所以OA、OB、OC都在平面OAB内，说明c与a、b共面。三个向量共面，又称这三个向量线性相关；反之，如果三个向量不共面，则称这三个向量线性无关。BOabCccA��线例1、如图，在空间四边形ABCD中，若AB、CD中点分别为E、F，判断EF与AD + BC是否共？��线。解：取AC中点G，连接EG、FG，111 EF = EG + GF =BC +AD =AD + BC222∴EF与AD + BC共CAFEDBG2ABCA B CAB,AC,ACBCMNAM,01 ,,ab AAck AC BNkBCkMNa c����例 、已知斜三棱柱－，使在面对角线上和棱上分别取点和 ，使≤ ≤求证：与向量共面。  ABCNABCM4. 共面向量定理等价说法MByMAxMPyxMABP使对...