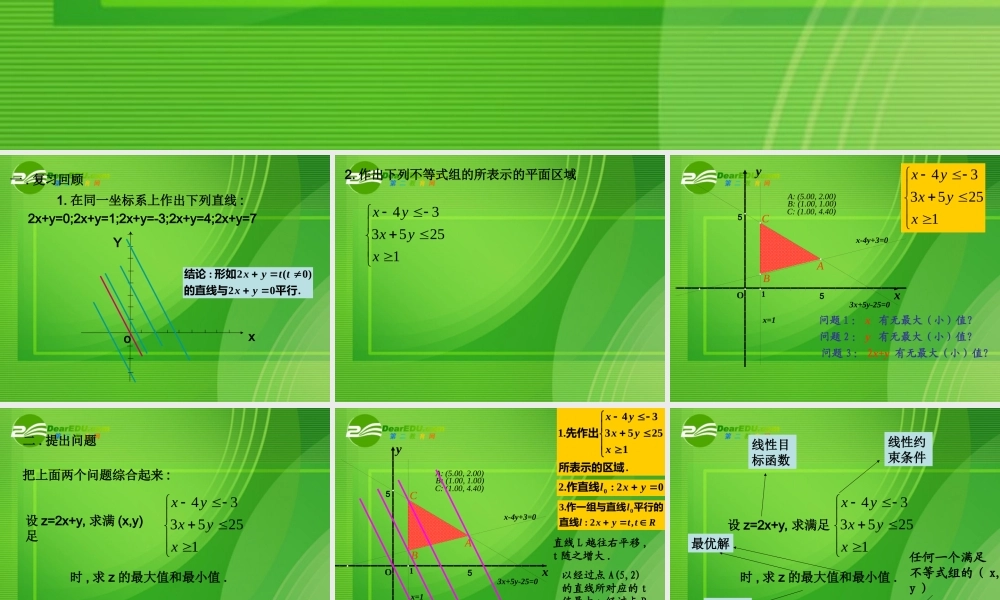
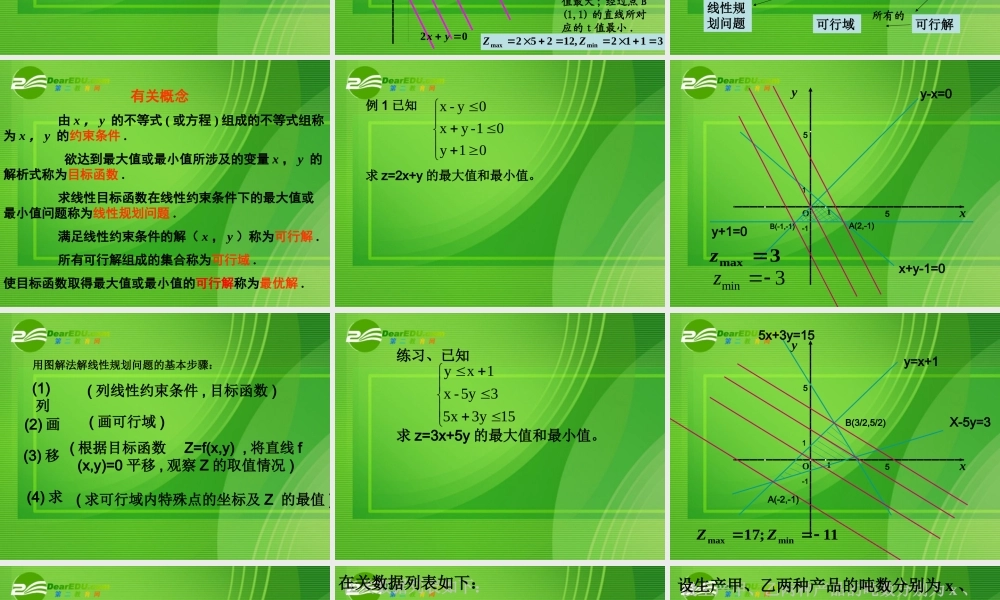
一 . 复习回顾1. 在同一坐标系上作出下列直线 :2x+y=0;2x+y=1;2x+y=-3;2x+y=4;2x+y=7.02)0(2:平行的直线与形如结论yxttyxxYo 2. 作出下列不等式组的所表示的平面区域1255334xyxyx 55x=1x-4y+3=03x+5y-25=01ABCC: (1.00, 4.40)A: (5.00, 2.00)B: (1.00, 1.00)Oxy问题 1 : x 有无最大(小)值?问题 2 : y 有无最大(小)值?问题 3 : 2x+y 有无最大(小)值?1255334xyxyx 二 . 提出问题把上面两个问题综合起来 :1255334xyxyx设 z=2x+y, 求满 (x,y)足时 , 求 z 的最大值和最小值 . 55x=1x-4y+3=03x+5y-25=01ABCC: (1.00, 4.40)A: (5.00, 2.00)B: (1.00, 1.00)Oxy.1255334.1所表示的区域先作出xyxyx02 yx02:.20 yxl作直线Rttyxll,2:.30直线平行的作一组与直线直线 L 越往右平移 ,t 随之增大 .以经过点 A(5,2)的直线所对应的 t值最大 ; 经过点 B(1,1) 的直线所对应的 t 值最小 .3112,12252minmaxZZ 1255334xyxyx设 z=2x+y, 求满足时 , 求 z 的最大值和最小值 .线性目标函数线性约束条件线性规划问题任何一个满足不等式组的( x,y )可行解可行域所有的最优解 有关概念 由 x , y 的不等式 ( 或方程 ) 组成的不等式组称为 x , y 的约束条件 . 欲达到最大值或最小值所涉及的变量 x , y 的解析式称为目标函数 . 求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题 . 满足线性约束条件的解( x , y )称为可行解 . 所有可行解组成的集合称为可行域 .使目标函数取得最大值或最小值的可行解称为最优解 . 例 1 已知求 z=2x+y 的最大值和最小值。01y01-yx0y-x 551Oxyy-x=0x+y-1=01-1y+1=0A(2,-1)B(-1,-1)3max zmin3z (1)列 (2) 画(3) 移 (4) 求( 列线性约束条件 , 目标函数 ) ( 画可行域 )( 根据目标函数 Z=f(x,y) , 将直线 f(x,y)=0 平移 , 观察 Z 的取值情况 ) ( 求可行域内特殊点的坐标及 Z 的最值 )用图解法解线性规划问题的基本步骤: 练习、已知求 z=3x+5y 的最大值和最小值。153y5x35y-x1xy 551Oxy1-15x+3y=15X-5y=3y=x+1A(-2,-1)B(3/2,5/2)11;17minmaxZZ ...