高二数学二项式定理题型荟萃 人教版 课件VIP免费

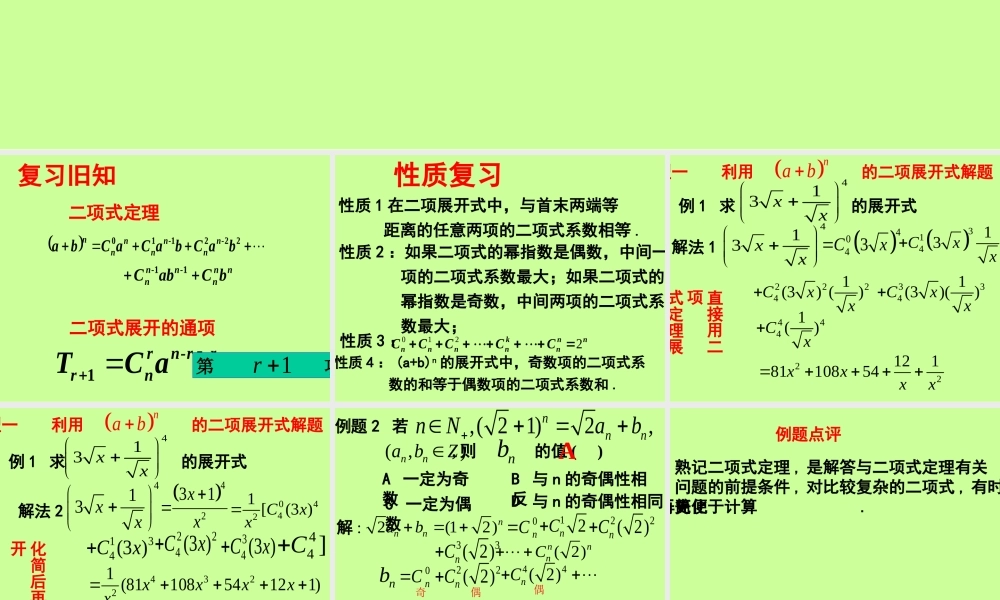
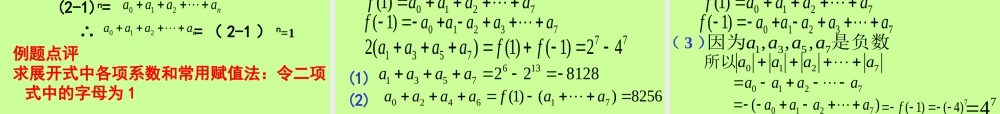二项式定理222110baCbaCaCba-nn-nnnnnnnn-n-nnbCabC11二项式展开的通项rr-nrnrbaCT1复习旧知第 项1r 性质复习性质 1 在二项展开式中，与首末两端等 距离的任意两项的二项式系数相等 .性质 2 ：如果二项式的幂指数是偶数，中间一 项的二项式系数最大；如果二项式的 幂指数是奇数，中间两项的二项式系 数最大；nnnknnnnCCCCC2210性质 3 ：性质 4 ： (a+b)n 的展开式中，奇数项的二项式系 数的和等于偶数项的二项式系数和 . 题型一 利用 的二项展开式解题nab解法 1413 xx404 3Cx例 1 求 的展开式413 xx31413Cxx22241(3) ()Cxx3341(3)()Cxx4441()Cx221218110854xxxx直接用二项式定理展开 题型一 利用 的二项展开式解题nab例 1 求 的展开式413 xx解法 2413 xx4231xx04421 [(3 )Cxx134(3 )Cx224 (3 )Cx34(3 )Cx44 ]C43221 (8110854121)xxxxx221218110854xxxx化简后再展开 例题 2 若,( 21)2,nnnnNab(,)nna bZnb, 则 的值 ( )A 一定为奇数C 一定为偶数B 与 n 的奇偶性相反D 与 n 的奇偶性相同解 :2(12)nnnab0nC1 2nC22( 2)nC33( 2)nC( 2)nnnCnb0nC22( 2)nC44( 2)nC所以 为奇数 故选(A)nb思考 能用特殊值法吗 ?偶偶奇A 熟记二项式定理 , 是解答与二项式定理有关问题的前提条件 , 对比较复杂的二项式 , 有时先化简再展开更便于计算.例题点评 题型二利用通项求符合要求的项或项的系数例 3 求 展开式中的有理项93xx解 :1132 919 ()()rrrrTC xx 2769( 1)rrrC x 令 273466rrZZ即(0,19)r 39rr 或3344492734( 1)846rrTC xx 99331092793( 1)6rrTC xx 原式的有理项为 :4484Tx310xT 例 4(04 全国卷 )81()xx的展开式中 的系数为 __________5x解 : 设第 项为所求1r 12818()rrrrTC xx 288( 1)rrrrC xx 3288( 1)rrrC x 38522rr由可得5x228( 1)28C的系数为 .)2(.510和第四项的系数项式系数的展开式中第四项的二求例xx 分析：第 k+1 项的二项式系数 --- 第 k+1 项...