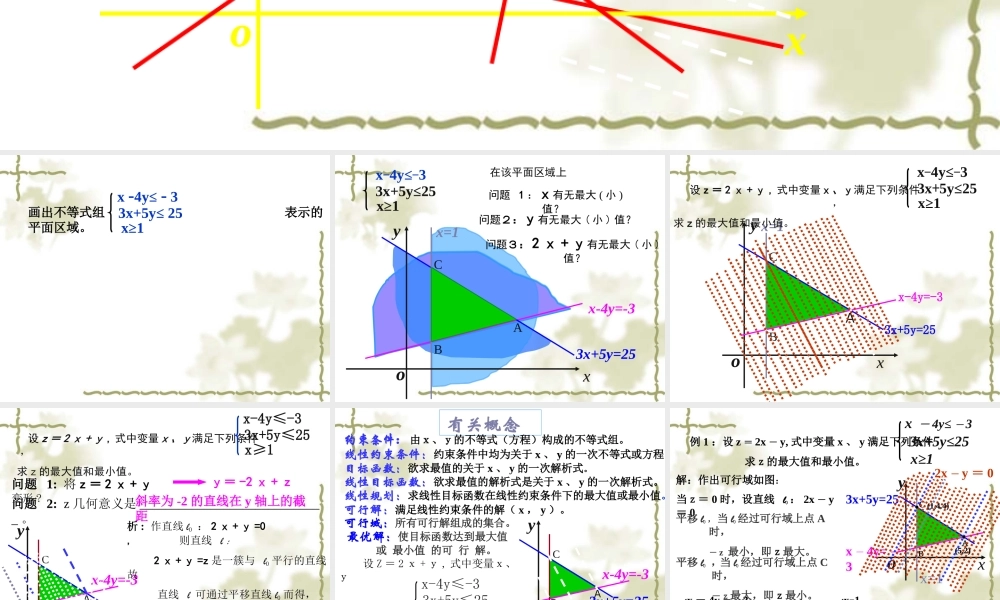
xyo画出不等式组 表示的平面区域。3x+5y≤ 25 x -4y≤ - 3x≥13x+5y≤25x-4y≤-3x≥1在该平面区域上 问题 1 :x有无最大 ( 小 )值?问题2:y有无最大 ( 小 ) 值?xyox-4y=-33x+5y=25x=1问题3: 2 x + y有无最大 ( 小 )值?CABxyox=1CB 设 z = 2 x + y , 式中变量x、y满足下列条件 ,求z的最大值和最小值。 3x+5y≤25x-4y≤-3x≥1Ax-4y=-33x+5y=25xyox-4y=-3x=1C 设 z = 2 x + y , 式中变量x、y满足下列条件 , 求z的最大值和最小值。 3x+5y≤25x-4y≤-3x≥1BA3x+5y=25问题 1: 将 z = 2 x + y变形 ?问题 2: z 几何意义是 _____________________________ 。斜率为 -2 的直线在 y 轴上的截距 则直线 l : 2 x + y =z 是一簇与 l0 平行的直线 ,故 直线 l 可通过平移直线 l0 而得,当直 线往右上方平移时 z 逐渐增大: 当 l 过点 B(1,1) 时 ,z 最小 , 即 zmin=3 当 l 过点 A(5,2) 时,z最大 , 即 zmax = 2×5+2 = 12 。 析 : 作直线 l0 : 2 x + y =0 , y= -2 x + z最优解:使目标函数达到最大值或 最小值 的可 行 解。 线性约束条件:约束条件中均为关于 x 、 y 的一次不等式或方程。有关概念 约束条件:由x、y的不等式(方程)构成的不等式组。目标函数:欲求最值的关于 x 、 y 的一次解析式。线性目标函数:欲求最值的解析式是关于 x 、 y 的一次解析式。线性规划:求线性目标函数在线性约束条件下的最大值或最小值。可行解:满足线性约束条件的解( x , y )。 可行域:所有可行解组成的集合。xyox-4y=-3x=1CBA3x+5y=25 设 Z = 2 x + y , 式中变量x、y 满足下列条件 , 求z的最大值和最小值。 3x+5y≤25x-4y≤-3x≥1B Cxyox - 4y= -33x+5y=25x=1A 例 1 :设 z = 2x - y, 式中变量 x 、 y 满足下列条件 求z的最大值和最小值。3x+5y≤25x - 4y≤ - 3x≥1解:作出可行域如图:当z= 0 时,设直线 l0 : 2x - y= 0 当 l0 经过可行域上点 A时,- z 最小,即z最大。 当 l0 经过可行域上点 C时,-z最大,即z最小。由 得 A 点坐标 _____ ; x - 4y =- 3 3x + 5y = 25由 得 C 点坐标_______ ; x=1 3x + 5y = 25 ∴ ∴zmax = 2×5 - 2 =...