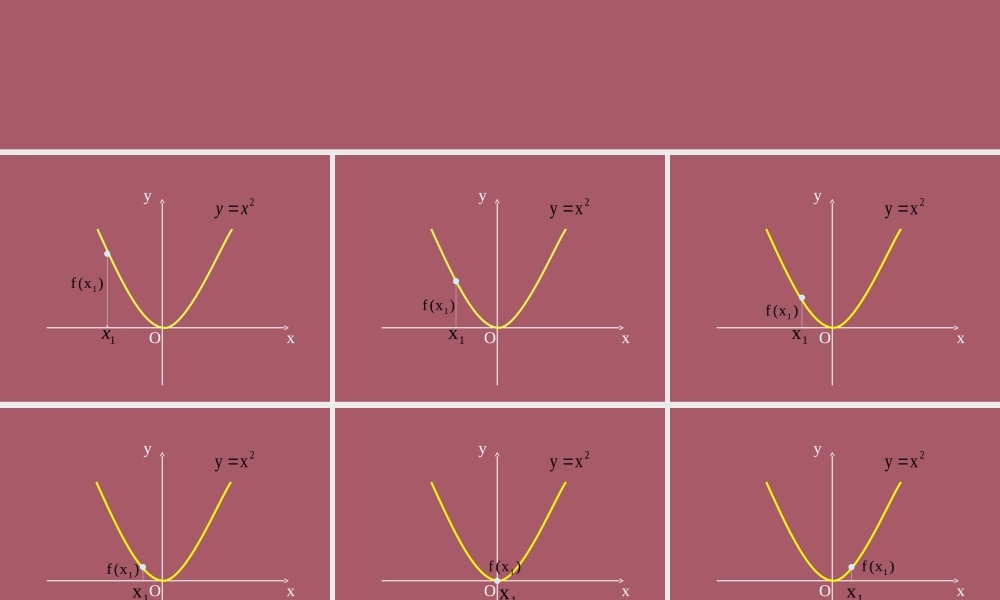
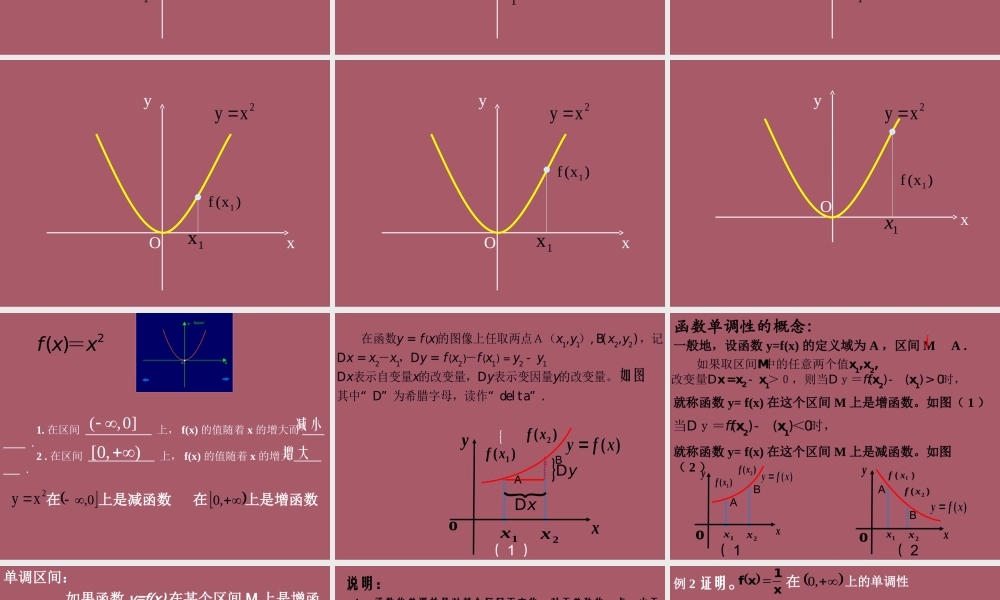
函数的单调性函数的单调性Oxy1x)x(f12xy Oxy1x)x(f12xy Oxy1x)x(f12xy Oxy1x)x(f12xy Oxy1x)x(f12xy Oxy1x)x(f12xy Oxy1x)x(f12xy Oxy1x)x(f12xy Ox)x(f11xy2xy 1. 在区间 ____________ 上, f(x) 的值随着 x 的增大而 ________ .2 . 在区间 ____________ 上, f(x) 的值随着 x 的增大 ________ .减小(,0] [0,)增大在2xy 0,上是减函数在,0上是增函数2( )f xx={xD)(1xf)(2xfxyoAB1x2x( 1 ){{yD1122212121( )()(),,yf xx yx yxxxyf xf xyyxxyy==D=D=-DDD 在函数的图像上任取两点A(), B(),记- ,-表示自变量 的改变量,表示变因量 的改变量。其中“” 为希腊字母,读作“ del ta” .如图函数单调性的概念:就称函数 y= f(x) 在这个区间 M 上是增函数。如图( 1 )一般地,设函数 y=f(x) 的定义域为 A ,区间 M A . Í()( )0ffD-D-> 如果取区间 中的任意两个值改变量>0,则当y=时,121212Mx ,x ,x=xxxx()( ) 0ffD-当y=< 时,21xx就称函数 y= f(x) 在这个区间 M 上是减函数。如图( 2 )y)(1xf)(2xfxoAB1x2x( 1)1x2x)(2xfxyo)(1xfAB( 2)单调区间: 如果函数 y=f(x) 在某个区间 M 上是增函数或是减函数,那么就说函数 y=f(x) 在这个区间M 上具有单调性,区间 M 称为 y=f(x) 的单调区间 . 说明: 1 、函数的单调性是对某个区间而言的,对于单独的一点,由于它的函数值是唯一确定的常数,因而没有增减变化,所以不存在单调性问题; 2 、中学阶段研究的主要是连续函数或分段连续函数,对于闭区间上的连续函数来说,只要在开区间上单调,它在闭区间上也就单调,因此,在考虑它的单调区间时,包括不包括端点都可以; 3 、对于在某些点上不连续的函数,单调区间不包括不连续点 .例 1 证明函数 f(x)=2x+1 在 (-∞,+∞) 上是增函数例 2 证明。 x1xf在 ,0上的单调性证明:()+¥设是上的任意两个实数12 x ,x0,,xx21 且()1212,0,,0,00,x xx xxyÎ+¥>D>D<由得又由于是 上是减函数在所以,01xxf2121()()xxxyf xf xD=D=-- >0,-则 =2111xxx-D== -121 21 2xxx xx x用定义证明函数单调性的步骤 证明函数 f(x) 在区间 M 上具有单调性的步骤:(1) 取值:对任意 x1 , x2M,∈且 x1 < x2 ,(2) 作差、变形:△ y ...