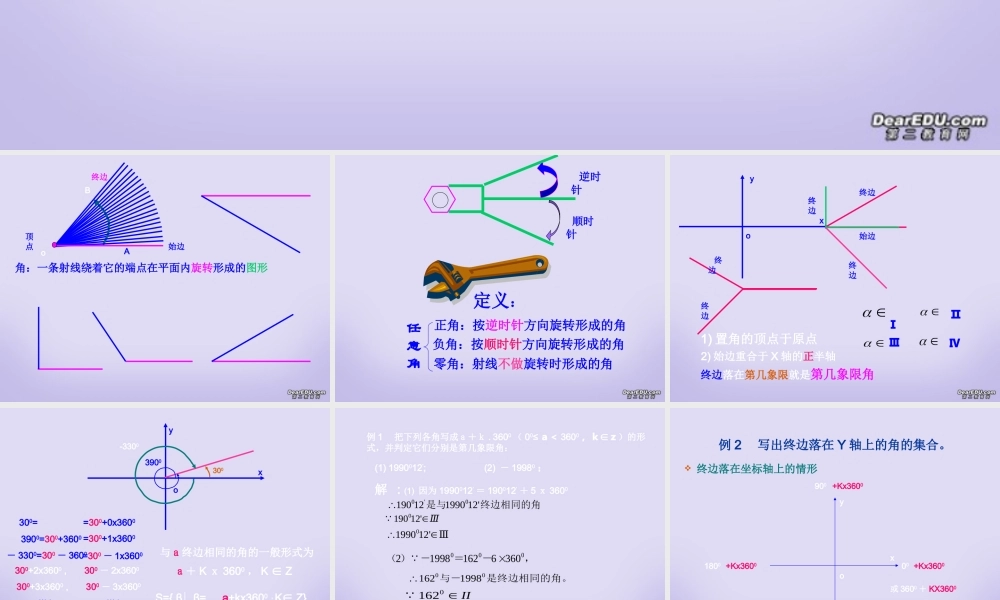
三角函数三角函数1.1.11.1.1 任意角任意角oAB始边 终边顶点角:一条射线绕着它的端点在平面内旋转形成的图形 逆时针 顺时针定义:正角:按逆时针方向旋转形成的角负角:按顺时针方向旋转形成的角 零角:射线不做旋转时形成的角任意角xyo始边 终边 终边终边终边1) 置角的顶点于原点终边落在第几象限就是第几象限角2) 始边重合于 X 轴的正半轴终边 Ⅰ Ⅱ Ⅲ Ⅳxy o3003900-33003900=300+3600- 3300=300 - 3600=300+1x3600 =300 - 1x3600 300= =300+0x3600300+2x3600 , 300 - 2x3600 300+3x3600 , 300 - 3x3600 … , … ,与 300 终边相同的角的一般形式为 300 + KX3600 , K ∈ Z与a终边相同的角的一般形式为a+ K x 3600 , K Z∈S={ β| β= a+kx3600 , K Z}∈例 1 把下列各角写成a+k .3600 ( 00≤ a< 3600 ,k∈z)的形式,并判定它们分别是第几象限角:(1) 1990012’; (2) - 19980 ; 解 : (1) 因为 1990012’ = 190012’ + 5 x 3600终边相同的角是与12'1990121900'0Ⅲ'121900 ,-=-) (000360616219982Ⅲ12'19900是终边相同的角。与-001998162II0162II01998 练习:课本 6 页 3 4 题 例 2 写出终边落在 Y 轴上的角的集合。 终边落在坐标轴上的情形xyo0090018002700 +Kx3600+Kx3600+Kx3600+Kx3600或 3600 + KX3600例 2 写出终边落在 y 轴上的角的集合。 解:终边落在y轴正半轴上的角的集合为S1={β| β=900+K∙3600,K∈Z} ={β| β=900+2K∙1800,KZ}∈={β| β=900+1800 的偶数倍 }终边落在y轴负半轴上的角的集合为S2={β| β=2700+K∙3600,KZ}∈={β| β=900+1800+2K∙1800,KZ}∈={β| β=900+ ( 2K+1 ) 1800 , KZ}∈={β| β=900+1800 的奇数倍 }S=S1∪S2所以 终边落在y轴上的角的集合为={β| β=900+1800 的偶数倍 }∪{β| β=900+1800 的奇数倍 }={β| β=900+1800 的整数倍 } ={β| β=900+K∙1800 , K∈Z}{偶数}∪{奇数}={整数}XYO900+K∙36002700+k∙3600练习 写出终边落在x轴上的角的集合变式 1 :写出终边落在直线 y=x 上的角的集合变式 2 :写出终边落在第一象限的角的集合 写出终边落在 轴上的角的集合。 解:终边落在 轴正半轴上的角的集合为S1={β| β= K∙3600,K∈Z} ={β...