高中数学 简单线性规划课件 苏教版必修5 课件VIP免费

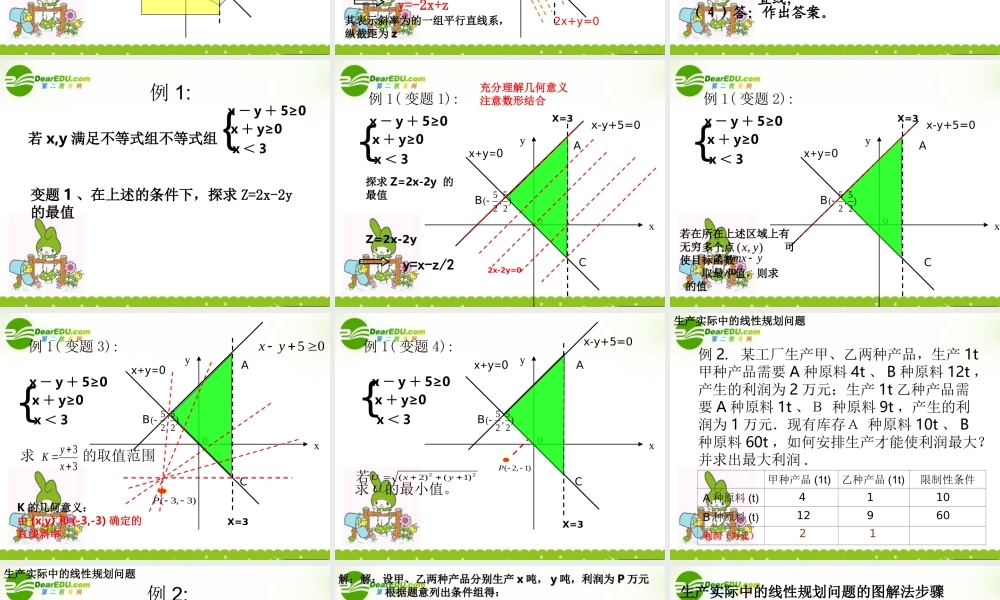
简单线性规划 ( 复习课 )复习目标：•会作二元一次不等式表示的平面区域•了解线性规划的意义，并会进行简单的应用基础训练1 、画出 x ＋ y ＋ 1 ＜ 0 表示的平面区域 xyo-1-1直线定界特殊点定域虚实分清作图准确规范2 、作出不等式组{ 表示的平面区域？x － y ＋ 5≥0x ＋ y≥0 x ＜ 3基础训练xyoABC{x － y ＋ 5≥0x ＋ y≥0 x ＜ 3x=3作出不等式组表示的平面区域x-y+5=0x+y=0xyo5 5(, )2 2ABC例 1: （线性规划问题）{x － y ＋ 5≥0x ＋ y≥0 x ＜ 3X=3求 Z=2x+y 的最小值z=2x+yy=-2x+z其表示斜率为的一组平行直线系，纵截距为 z若 x,y 满足线性约束条件最优解目标函数可行域可行解解决此类问题的一般步骤？x-y+5=0x+y=02x+y=0解线性规划问题的步骤（ 2 ）移：在线性目标函数所表示的一组平行 线中，利用平移的方法找出与可行 域有公共点且纵截距最大或最小的 直线； （ 3 ）求：通过解方程组求出最优解； （ 4 ）答：作出答案。 （ 1 ）画：画出线性约束条件所表示的可行域；若 x,y 满足不等式组不等式组{ 例 1:变题 1 、在上述的条件下，探求 Z=2x-2y 的最值x － y ＋ 5≥0x ＋ y≥0 x ＜ 3xyoABC5 5(, )2 2例 1( 变题 1):探求 Z=2x-2y 的最值2x-2y=0Z=2x-2yy=x-z/2充分理解几何意义注意数形结合{x － y ＋ 5≥0x ＋ y≥0 x ＜ 3x+y=0x-y+5=0X=3xyoABC5 5(, )2 2例 1( 变题 2):{x － y ＋ 5≥0x ＋ y≥0 x ＜ 3x+y=0x-y+5=0X=3若在所在上述区域上有无穷多个点 可使目标函数 取最小值，则求 的值 ( , )x yZmxymxyoABC5 5(, )2 2例 1( 变题 3):50xy求33yKx 的取值范围 ( 3, 3)P K 的几何意义：由 (x,y) 和 (-3,-3) 确定的直线斜率{x － y ＋ 5≥0x ＋ y≥0 x ＜ 3X=3x+y=0xyoABC5 5(, )2 2例 1( 变题 4):( 2, 1)P U若求的最小值。 22)1()2(yxUx-y+5=0x+y=0X=3x － y ＋ 5≥0x ＋ y≥0 x ＜ 3{例 2. 某工厂生产甲、乙两种产品，生产 1t甲种产品需要 A 种原料 4t 、 B 种原料 12t ，产生的利润为 2 万元；生产 1t 乙种产品需要 A 种原料 1t 、Ｂ 种原料 9t ，产生的利润为 1 万元．现有库存Ａ 种原料 10t 、 B种原料 60t ，如何安排生产才能使利润最大？并求出最大利润 . 甲种产品 (1t)乙...