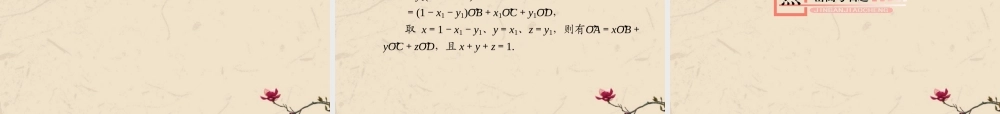最新考纲解读1 .理解空间向量的概念,掌握空间向量的四种运算.2 .了解空间向量的基本定理.3 .掌握空间向量的数量积的定义及其性质.4 .掌握空间向量平行、垂直的条件及三个向量共面及四点共面的条件.高考考查命题趋势向量由于具有几何形式和代数形式的“双重身份”,使它成为中学数学知识的一个交汇点,成为联系多项内容的媒介.空间向量是处理空间问题的重要方法,通过将空间元素间的位置关系转化为数量关系,将过去的形式逻辑证明转化为数值计算,化繁难为简易,化复杂为简单,是一种重要的解决问题的手段和方法.因为各学校采用教材版本不同,高考中不会单独命题考查 .1. 空间向量的概念:在空间,我们把具有大小和方向的量叫做向量.注: (1) 空间的一个平移就是一个向量.(2) 向量一般用有向线段表示,同向等长的有向线段表示同一或相等的向量.(3) 空间的两个向量可用同一平面内的两条有向线段来表示.2.空间向量的运算:空间向量的加法、减法与数乘向量运算: OB→ =OA→ +AB→=a+b;BA→=OA→-OB→ =a-b; OP→ =λa(λ∈R). 3.共线向量 方向相同或者相反的非零向量叫做平行向量.也叫做共线向量. 当我们说向量 a、b 共线(或 a∥b)时,表示 a、b 的有向线段所在的直线可能是同一直线,也可能是平行直线. 4.共线向量定理:空间任意两个向量 a、b(b≠0),a∥b 的充要条件是存在实数 λ,使 a=λb. 推论:如果 l 为经过已知点 A 且平行于已知非零向量的直线,那么对于任意一点 O,点 P 在直线 l 上的充要条件是存在实数 t 满足等式OP→ =OA→ +ta. 其中向量 a 叫做直线 l 的方向向量. 5.空间直线的向量参数表示式: OP→ =OA→ +ta 或OP→ =OA→ +t(OB→ -OA→ )=(1-t)OA→ +tOB→ , 中点公式:OP→ =12(OA→ +OB→ ). 6.向量与平面平行:已知平面 α 和向量 a,作OA→ =a,如果直线 OA 平行于 α 或在 α 内,那么我们说向量 a平行于平面 α,记作:a∥α.通常我们把平行于同一平面的向量,叫做共面向量. 说明:空间任意的两向量都是共面的. 7.共面向量定理:如果两个向量 a,b 不共线,p与向量 a,b 共面的充要条件是存在实数 x,y,使 p=xa+yb. 推论:空间一点 P 在平面 MAB 内的充分必要条件是存在有序实数对 x,y,使MP→ =xMA→ +yMB→ ① 或对空间任一点 O,有OP→ =OM→ +xMA→...