简单的线性规划 人教版2 课件VIP免费

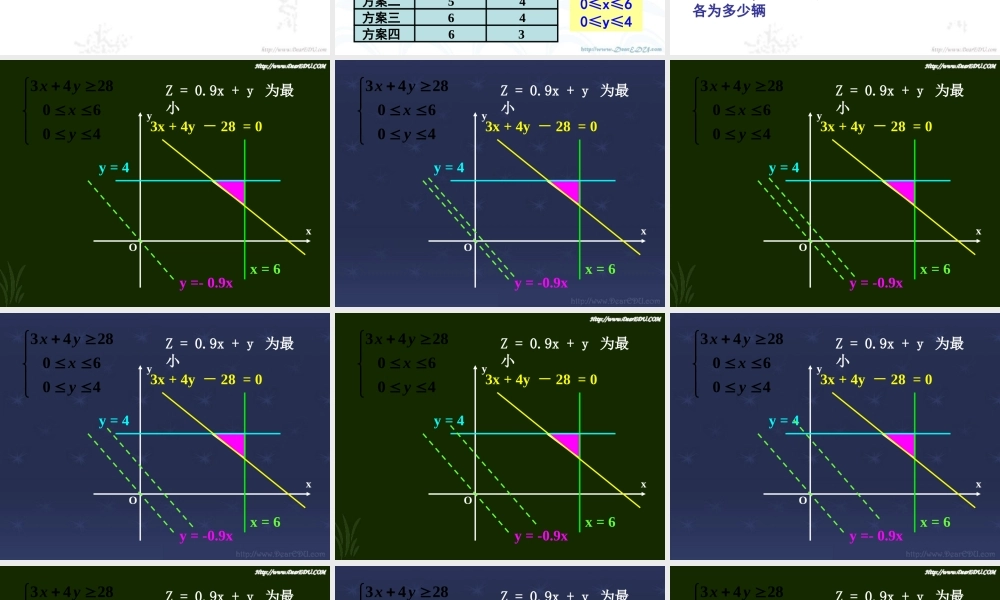
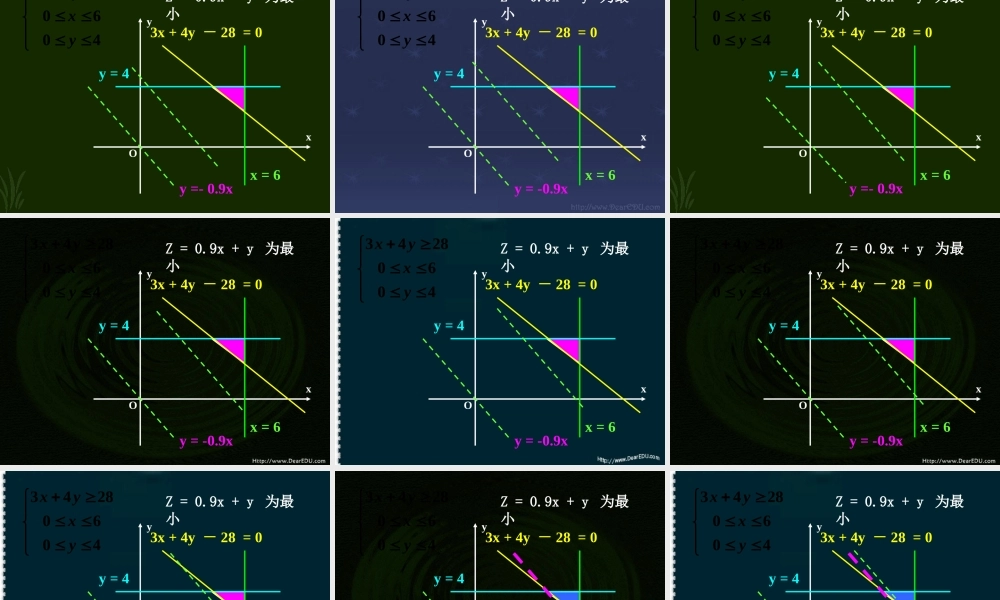
1. 画出下列不等式所表示的平面区域：① 4x-3y≤12② x≥1③ x-2y<0④ -2x+y-3>0 1xoy21xoy3xoy3xoy－ 4 注意：② 至于是哪一侧的区域的判断方法： ① 若“ >” 或“ <” 则把直线画成虚线；若“≥”或“≤” 则把直线画成实线 由于对直线同一侧的所有点 (x,y) ，把它代入 Ax+By+C ，所得实数的符号都相同，所以只需在此直线的某一侧取一个特殊点 (x0,y0) ，从 Ax0+By0+C的正负可以判断出 Ax+By+C>0 表示哪一侧的区域。一般在 C≠0 时，取原点作为特殊点 总结归纳：直线定界，特殊点定域C≠0 时，取原点作为特殊点C ＝ 0 时，取（ 0 ， 1 ）作为特殊点 例 5 。某公司承担了每天至少搬运 280t 水泥的任务，已知该公司有 6 辆 A 型卡车和 4 辆 B 型卡车，已知 A 型卡车每天每辆的运载量为 30t ，成本费为 0.9 千元， B型卡车每天每辆的运载量为 40t ，成本费为 1 千元。（ 1 ）假设你是公司的调度员，请你按要求设计出公司每天的排车方案。（ 2 ）设每天派出 A 型卡车 x 辆， B 型卡车 y 辆，公司每天花费成本为 Z 千元，写出 x 、 y 应满足的条件以及Z 与 x 、 y 之间的函数关系式。方案方案一方案二方案三方案四A 型卡车B 型卡车44546463Z= 0.9x + y3x+4y≥280≤x≤60≤y≤4 1 、某公司承担了每天至少搬运 280t 水泥的任务，已知该公司有 6 辆 A 型卡车和 4 辆 B 型卡车，已知A 型卡车每天每辆的运载量为 30t ，成本费为 0.9 千元， B 型卡车每天每辆的运载量为 40t ，成本费为 1千元。（ 1 ）假设你是公司的调度员，请你按要求设计出公司每天的排车方案。设每天派出 A 型卡车 x 辆， B 型卡车y 辆，（ 2 ）若公司每天花费成本为 Z 千元，写出 x 、 y 应满足的条件以及 Z 与 x 、 y 之间的函数关系式。(3)如果你是公司的经理，为使公司所花的成本费最小，每天应派出 A 型卡车、 B 型卡车各为多少辆 Z = 0.9x + y 为最小Oyx40602843yxyxx = 6y = 43x + 4y － 28 = 0y =- 0.9x Oyx40602843yxyxx = 6y = 43x + 4y － 28 = 0y = -0.9xZ = 0.9x + y 为最小 Oyx40602843yxyxx = 6y = 43x + 4y － 28 = 0y = -0.9xZ = 0.9x + y 为最小 Oyx40602843yxyxx...