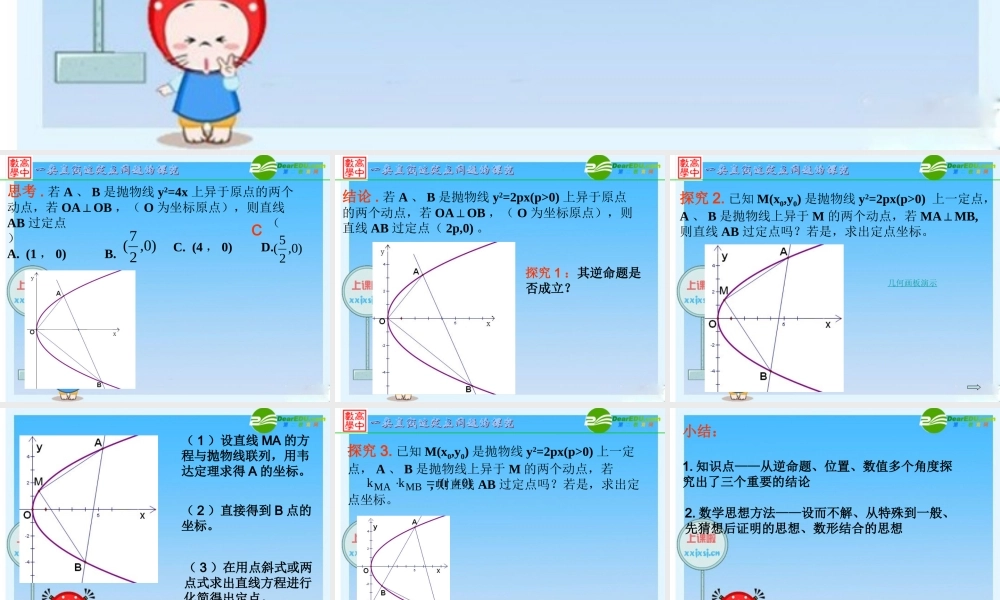
)0,27()0,25(思考 . 若 A 、 B 是抛物线 y2=4x 上异于原点的两个动点,若 OAOB⊥,( O 为坐标原点),则直线AB 过定点()A. (1 , 0) B. C. (4 , 0) D. C 结论 . 若 A 、 B 是抛物线 y2=2px(p>0) 上异于原点的两个动点,若 OAOB⊥,( O 为坐标原点),则直线 AB 过定点( 2p,0) 。探究 1 :其逆命题是否成立? 探究 2. 已知 M(x0,y0) 是抛物线 y2=2px(p>0) 上一定点,A 、 B 是抛物线上异于 M 的两个动点,若 MAMB,⊥则直线 AB 过定点吗?若是,求出定点坐标。几何画板演示 ( 1 )设直线 MA 的方程与抛物线联列,用韦达定理求得 A 的坐标。( 2 )直接得到 B 点的坐标。( 3 )在用点斜式或两点式求出直线方程进行化简得出定点。几何画板演示 探究 3. 已知 M(x0,y0) 是抛物线 y2=2px(p>0) 上一定点, A 、 B 是抛物线上异于 M 的两个动点,若 , 则直线 AB 过定点吗?若是,求出定点坐标。)0r(rkkMBMA 小结:1. 知识点——从逆命题、位置、数值多个角度探究出了三个重要的结论2. 数学思想方法——设而不解、从特殊到一般、先猜想后证明的思想、数形结合的思想 作业 . 如图:椭圆的两个焦点 F1,F2 与短轴两端点B1,B2 构成为∠ B2F1B1=1200 ,面积为 的菱形(1) 求椭圆的方程 ;(2) 若直线 与椭圆相交于 M,N 两点( M,N 不是左右顶点),且以 MN 为直径的圆过椭圆右定点 A 。求证:直线 l 过定点,并求出该定点的坐标。 32OyxBBFF1122AMN根据绍兴市的第一次统测题,给予继续深入的探究,课后尝试一下。mkxy:l