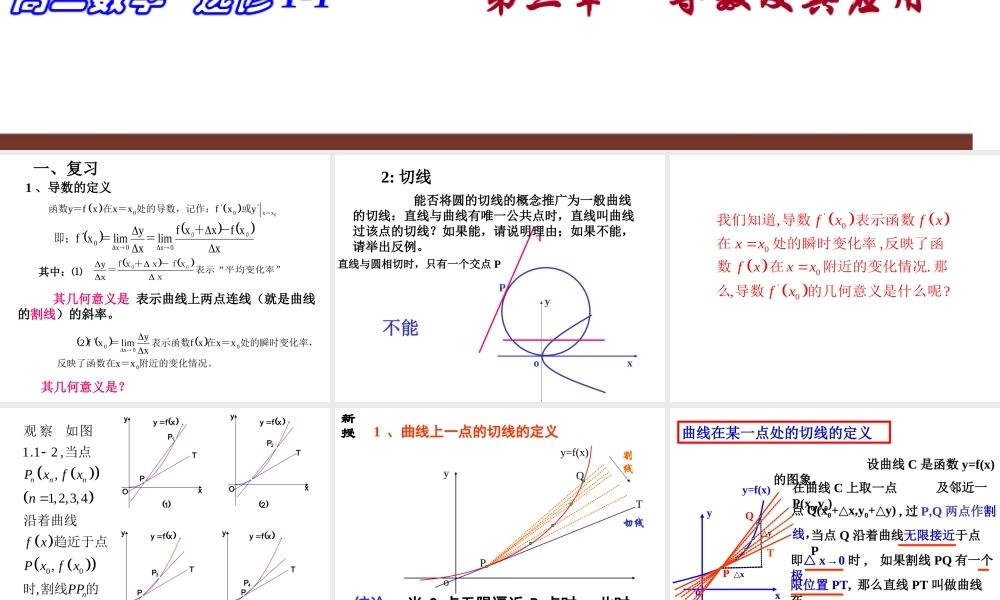
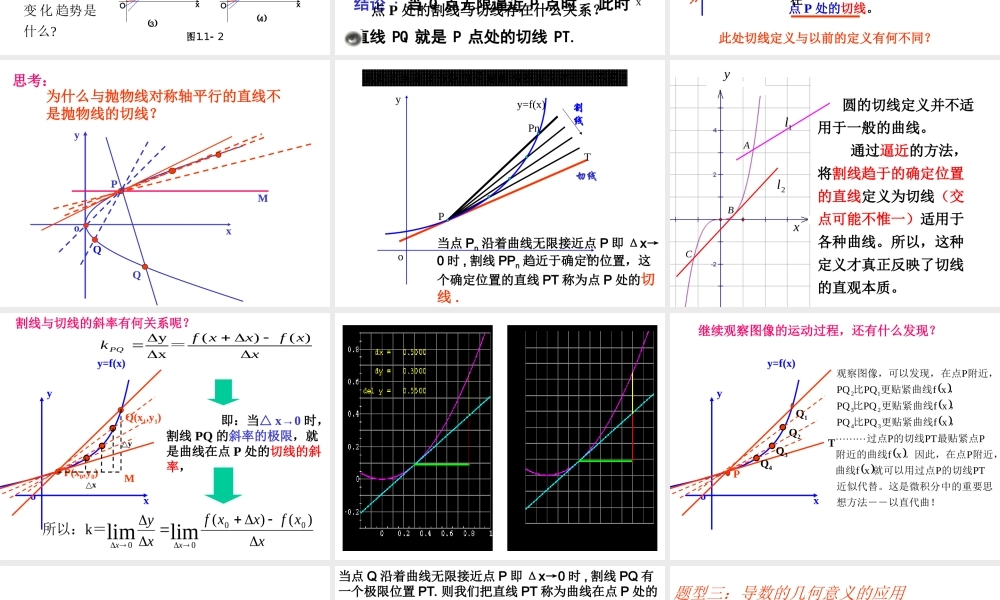
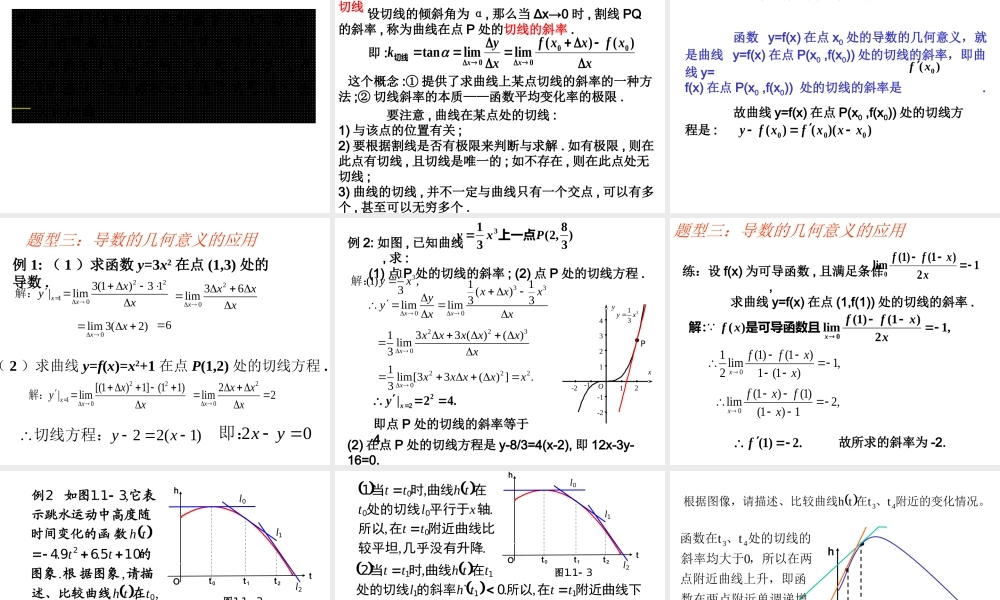
3.1.3 导数的 几何意义1高二数学 选修 1-1 第三章 导数及其应用 xxfxxflimxylimxf0x0x000-+==即: 000xxyf xxxfxy=函数 =在 =处的导数,记作:或表示“平均变化率”xx-fx+xf=00xy 附近的变化情况。=反映了函数在处的瞬时变化率,=在表示函数=000x0xxxxxfxylimxf2 一、复习1 、导数的定义其中:⑴ 其几何意义是 表示曲线上两点连线(就是曲线的割线)的斜率。其几何意义是? 2: 切线Pl 能否将圆的切线的概念推广为一般曲线的切线:直线与曲线有唯一公共点时,直线叫曲线过该点的切线?如果能,请说明理由;如果不能,请举出反例。不能xyo直线与圆相切时,只有一个交点 P '000'0,,.,?fxfxxxfxxxfx我们知道 导数表示函数在处的瞬时变化率 反映了函数在附近的变化情况 那么 导数的几何意义是什么呢 P1P2P3P4PTTTTPP xfy xfy xfy xfy OyxOyxOyxOyx211 .图 1 2 3 4 001.1 2 ,,1,2,3,4,,?nnnnPxf xnf xP xf xPP观 察如图当点沿着曲线趋近于点时 割线的变 化 趋势是什么 PQoxyy=f(x)割线切线T1 、曲线上一点的切线的定义结论 : 当 Q 点无限逼近 P 点时 , 此时直线 PQ 就是 P 点处的切线 PT.点 P 处的割线与切线存在什么关系?新授 xoyy=f(x) 设曲线 C 是函数 y=f(x)的图象,在曲线 C 上取一点P(x0,y0)及邻近一点 Q(x0+ x,y△0+ y)△, 过 P,Q 两点作割线,当点 Q 沿着曲线无限接近于点P点 P 处的切线。即△ x→0 时 , 如果割线 PQ 有一个极限位置 PT, 那么直线 PT 叫做曲线在曲线在某一点处的切线的定义△x△yPQT此处切线定义与以前的定义有何不同? xyoPQM为什么与抛物线对称轴平行的直线不是抛物线的切线? 思考:Q PPnoxyy=f(x)割线切线T当点 Pn 沿着曲线无限接近点 P 即 Δx→0 时 , 割线 PPn 趋近于确定的位置,这个确定位置的直线 PT 称为点 P 处的切线 .?同过的切线定义有什么不此处切线定义与以前学 圆的切线定义并不适用于一般的曲线。 通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。 2l1lxyABC xoyy=f(x)P(...