导数的意义及应用 苏教版 课件VIP免费

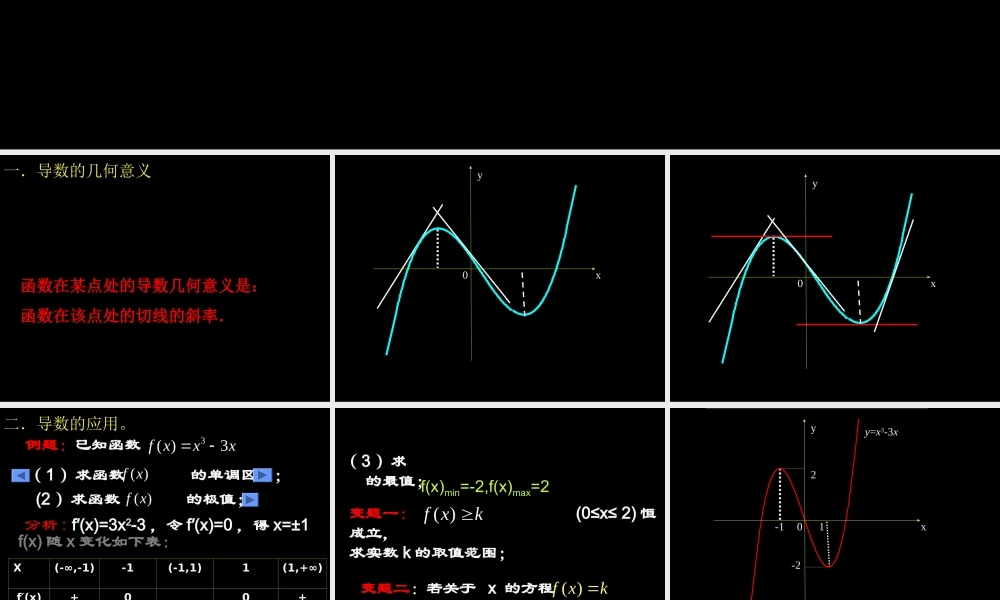
导数的意义及应用一．导数的几何意义.),3,1(1:3的值求相切于点与曲线直线问题bAbaxxykxy函数在某点处的导数几何意义是：函数在该点处的切线的斜率．1x2x0xy1x2x0xy例题：已知函数（ 1 ）求函数 的单调区间；3( )3f xxx( )f x分析 :(f′(x)=3x2-3 ，令 f′(x)=0 ，得 x=±1f(x) 随 x 变化如下表：X (-∞,-1)-1(-1,1)1(1,+∞)f′(x)+0_0+f(x)极大值：2极小值： -2(2 ）求函数 的极值；( )f x二．导数的应用。（ 3 ）求 的最值； 上０，２在区间)(xf变题一： (0≤x≤ 2) 恒成立，求实数 k 的取值范围；( )f xk( )f xk变题二：若关于 x 的方程 恒有 3 个不等实根，求实数 K 的取值范围。f(x)min=-2,f(x)max=2-2 y=x3-3x20xy33-11 f(x)=x3-3x2-20xy33-112上的最小值呢？变题三：区间为)0(a0,a最大值呢？ f(x)=x3-3x2-20xy33-112（ 4) ：求曲线 y=f(x) 在点 A （ 2 ， 2 ）处的切线方程。 （若改为过 A(2,2) 作曲线切线呢？）若改为过点 B （ 0,16 ）呢？10,)2()(2.23axaaxaxxf例(1)f(x) 在 R 上存在两个极值点 , 求 a 的取值范围 ;(2)f(x) 在 R 不存在极值点 , 求 a 的取值范围 .xf/(x)o++-x1x2x00,)1(2)(2.23axaaxaxxf例变题一： f(x) 在（ 0,1 ）上有两个极值点，求 a 的取值范围。变题二： f(x) 在（－ 1,0 ）上有一个极值点，在（ 0,1 ）上也有一个极值点 ,求 a 的取值范围。xof/(x)x0--x1x2＋思考题 . 已知函数 f(x)=(x-a)(x-b)(x-c) 。若 a>b>c ，且 f(x) 有两个极值点 x1 、 x2（ x1