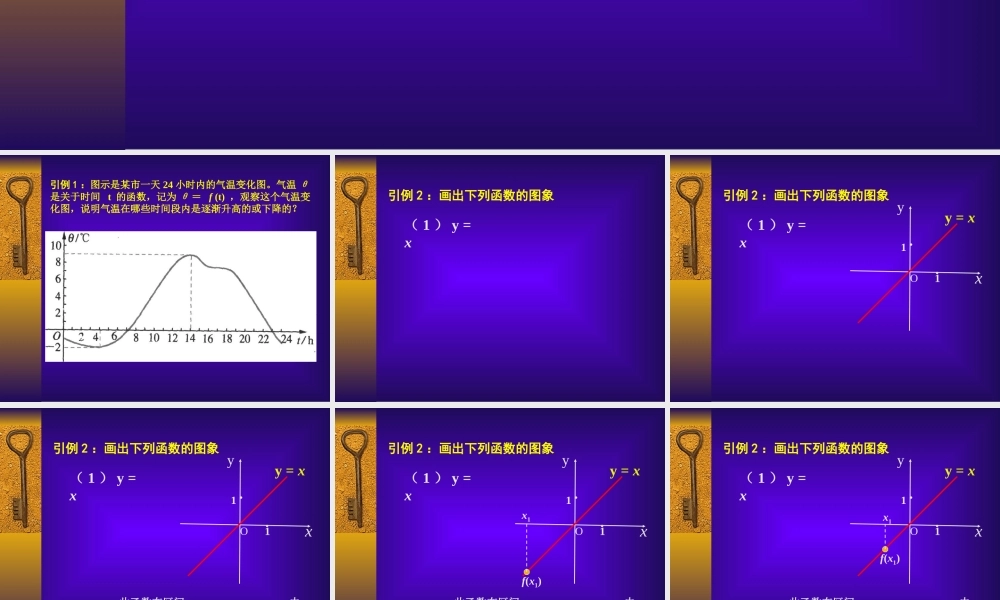
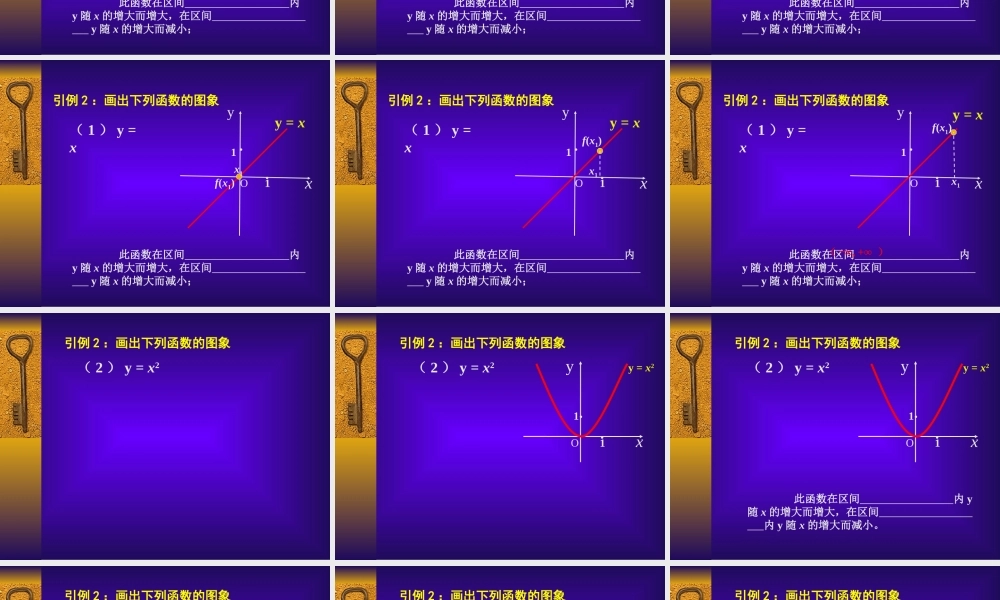
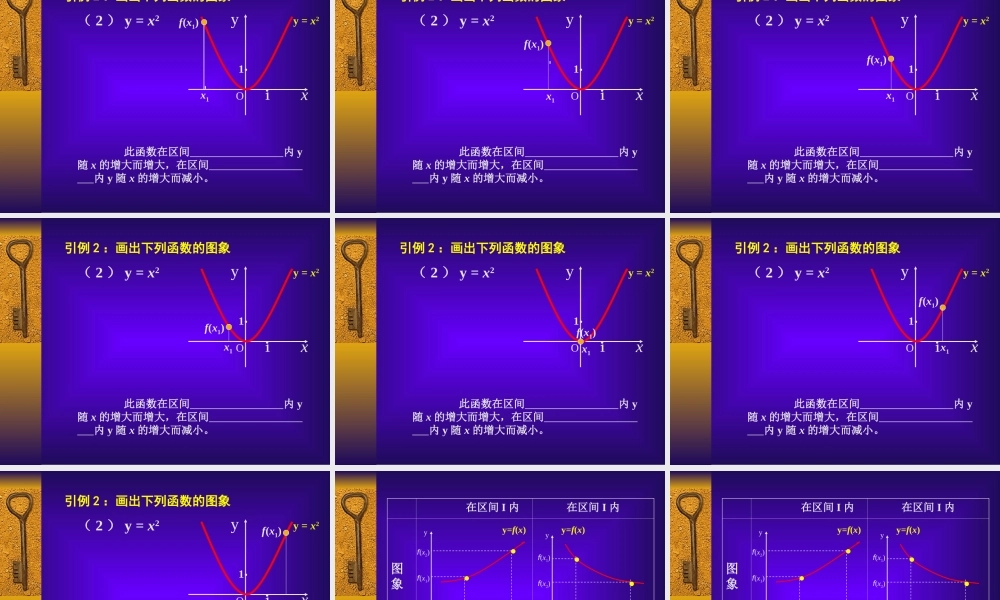
§2.1.3 函数的简单性质( 函数的单调性 ) 引例 1 :图示是某市一天 24 小时内的气温变化图。气温 θ是关于时间 t 的函数,记为 θ = f (t) ,观察这个气温变化图,说明气温在哪些时间段内是逐渐升高的或下降的? 引例 2 :画出下列函数的图象( 1 ) y = x xyy = xO11··引例 2 :画出下列函数的图象( 1 ) y = x xyy = xO11··引例 2 :画出下列函数的图象( 1 ) y = x 此函数在区间 内y 随 x 的增大而增大,在区间 y 随 x 的增大而减小; xyy = xO11··引例 2 :画出下列函数的图象( 1 ) y = x 此函数在区间 内y 随 x 的增大而增大,在区间 y 随 x 的增大而减小;x1f(x1) xyy = xO11··引例 2 :画出下列函数的图象( 1 ) y = x 此函数在区间 内y 随 x 的增大而增大,在区间 y 随 x 的增大而减小;x1f(x1) xyy = xO11··引例 2 :画出下列函数的图象( 1 ) y = x 此函数在区间 内y 随 x 的增大而增大,在区间 y 随 x 的增大而减小;x1f(x1) xyy = xO11··引例 2 :画出下列函数的图象( 1 ) y = x 此函数在区间 内y 随 x 的增大而增大,在区间 y 随 x 的增大而减小;x1f(x1) xyy = xO11··引例 2 :画出下列函数的图象( 1 ) y = x 此函数在区间 内y 随 x 的增大而增大,在区间 y 随 x 的增大而减小;x1f(x1)( -∞, +∞ ) ( 2 ) y = x2引例 2 :画出下列函数的图象 Oxyy = x2( 2 ) y = x2引例 2 :画出下列函数的图象1·1· Oxyy = x2( 2 ) y = x2引例 2 :画出下列函数的图象1·1· 此函数在区间 内 y随 x 的增大而增大,在区间 内 y 随 x 的增大而减小。 Oxyy = x2( 2 ) y = x2引例 2 :画出下列函数的图象1·1· 此函数在区间 内 y随 x 的增大而增大,在区间 内 y 随 x 的增大而减小。x1f(x1) Oxyy = x2( 2 ) y = x2引例 2 :画出下列函数的图象1·1· 此函数在区间 内 y随 x 的增大而增大,在区间 内 y 随 x 的增大而减小。f(x1)x1 Oxyy = x2( 2 ) y = x2引例 2 :画出下列函数的图象1·1· 此函数在区间 内 y随 x 的增大而增大,在区间 内 y 随 x 的增大而减小。f(x1)x1 Oxyy = x2( 2 ) y = x2引例 2 :画出下列函数的图象1·1...