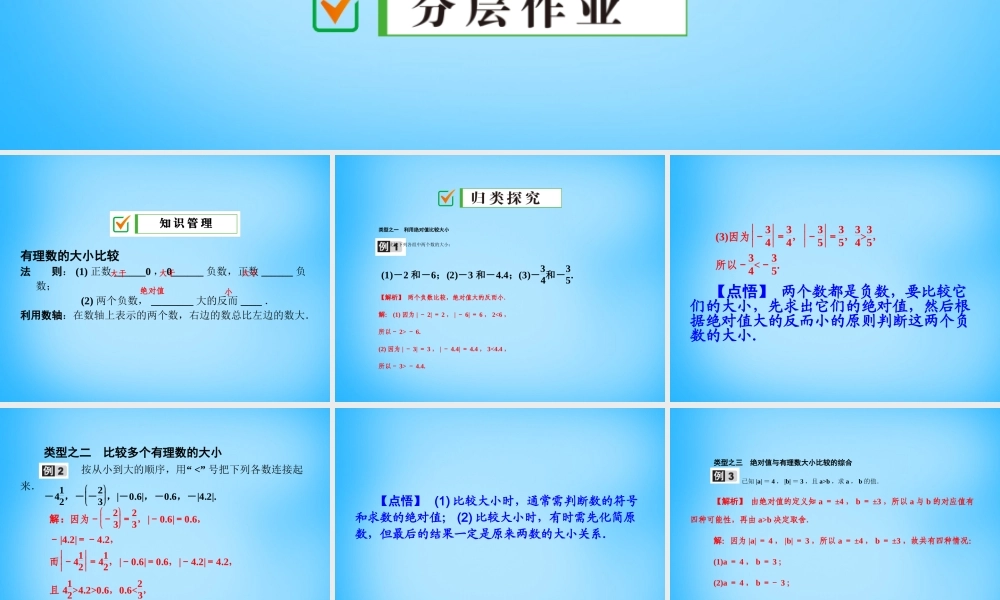
知 识 管 理第 2 课时 有理数的大小比较有理数的大小比较法 则: (1) 正数 ______0 , 0______ 负数,正数 ______ 负数; (2) 两个负数, ________ 大的反而 ____ .利用数轴:在数轴上表示的两个数,右边的数总比左边的数大.知 识 管 理 大于大于大于绝对值小类型之一 利用绝对值比较大小 比较下列各组中两个数的大小:【解析】 两个负数比较,绝对值大的反而小.解: (1) 因为 | - 2| = 2 , | - 6| = 6 , 2<6 ,所以- 2> - 6.(2) 因为 | - 3| = 3 , | - 4.4| = 4.4 , 3<4.4 ,所以- 3> - 4.4.(1)-2 和-6;(2)-3 和-4.4;(3)-34和-35. 【点悟】 两个数都是负数,要比较它们的大小,先求出它们的绝对值,然后根据绝对值大的反而小的原则判断这两个负数的大小.(3)因为-34 =34,-35 =35,34>35, 所以-34<-35. 类型之二 比较多个有理数的大小 按从小到大的顺序,用“ <” 号把下列各数连接起来.-412,--23 ,|-0.6|,-0.6,-|4.2|. 解:因为--23 =23,|-0.6|=0.6, -|4.2|=-4.2, 而-412 =412,|-0.6|=0.6,|-4.2|=4.2, 且 412>4.2>0.6,0.6<23, 所以-412<-|4.2|<-0.6<|-0.6|<--23 . 【点悟】 (1) 比较大小时,通常需判断数的符号和求数的绝对值; (2) 比较大小时,有时需先化简原数,但最后的结果一定是原来两数的大小关系.类型之三 绝对值与有理数大小比较的综合 已知 |a| = 4 , |b| = 3 ,且 a>b ,求 a , b 的值.【解析】 由绝对值的定义知 a = ±4 , b = ±3 ,所以 a 与 b 的对应值有四种可能性,再由 a>b 决定取舍.解:因为 |a| = 4 , |b| = 3 ,所以 a = ±4 , b = ±3 ,故共有四种情况:(1)a = 4 , b = 3 ;(2)a = 4 , b =- 3 ;(3)a =- 4 , b = 3 ;(4)a =- 4 , b =- 3.又因为 a>b ,所以只有 (1)(2) 两种情况符合题意,所以 a = 4 , b = 3 或 a = 4 , b =- 3.【点悟】 (1) 求 |a| = 4 时注意 a 的值有两个,即 a = ±4 ; (2) 解题时运用分类讨论的数学思想.1 . [2013· 重庆 ] 在 3 , 0 , 6 ,- 2 这四个数中,最大的...