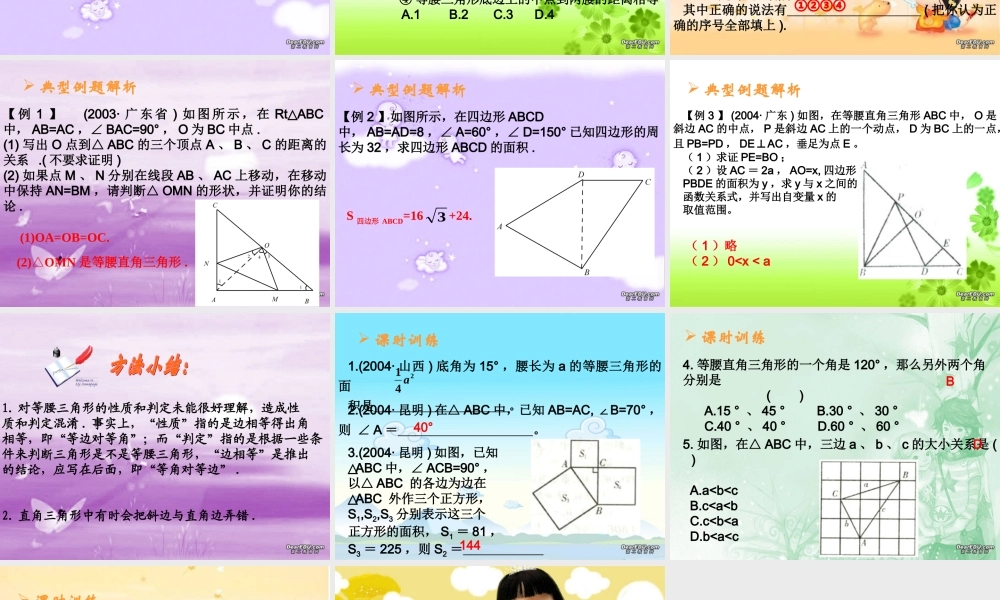
第四章第三课时: 等腰三角形及 直角三角形 要点、考点聚焦 课前热身 典型例题解析 课时训练 要点、考点聚焦1. 等腰三角形的性质定理及推论 1) 定理:等腰三角形的两个底角相等 ( 等边对等角 ). 2) 推论 1 :等腰三角形的顶角平分线平分底边并且 垂直于底边 ( 即等腰三角形三线合一 ). 推论 2 :等边三角形的各角都相等,并且每个角 都等于 60°. 2. 等腰三角形的判定定理及推论(1) 定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等 ( 简写成:等角对等边 ).(2) 推论 1 :三个角都相等的三角形是等边三角形 .推论 2 :有一个角是 60° 的等腰三角形是等边三角形 .推论 3 :在直角三角形中,如果一个锐角等于 30° ,那么它所对的直角边等于斜边的一半 .3. 勾股定理:直角三角形两直角边的平方和等于斜边的 平方,即 c2=a2+b2(c 为斜边 ).4. 勾 股 定 理 的 逆 定 理 : 如 果 三 角 形 的 三 边 长a 、 b 、 c ,有下面关系: a2+b2=c2 ,那么这个三角形是直角三角形. 要点、考点聚焦 课前热身BC1. 如果一个三角形的一个内角等于其他两个内角的差,那么这个三角形是 ( ) A. 等腰三角形 B. 直角三角形 C. 锐角三角形 D. 钝角三角形2. 一个直角三角形两边的长分别为 15 、 20 ,则第三边的长是 ( ) A. B.25 C. 或 25 D. 无法确定75753. 如果等腰三角形底边上的高等于腰长的一半,那么这个等腰三角形的顶角为 ( ) A.30° B.60° C.150 ° D.120°D4. 在下列四个命题中,正确的命题的个数是 ( ) ① 等腰三角形两腰上的中线相等 ② 等腰三角形两腰上的高相等 ③ 等腰三角形两底角的平分线相等 ④ 等腰三角形底边上的中点到两腰的距离相等 A.1 B.2 C.3 D.4D 课前热身①②③④5. 在△ ABC 中,如果只给出条件∠ A=60° ,那么还不能判定△ ABC 是等边三角形,给出下列四种说法:① 如果再加上条件: AB=AC ,那么△ ABC 是等边三角形② 如果再加上条件: tanB=tanC ,那么△ ABC 是等边三角形③ 如果再加上条件: D 是 BC 的中点,且 ADBC⊥,则△ ABC 是等边三角形④ 如果再加上条件: AB 、 AC 边上的高相等,那么△ ABC 是等边三角形其中正确的说法有 ( 把你认为正确的序号全部填上 ). 课前热身 典型例题解析(1)OA=OB=OC. 【 例 1 】...