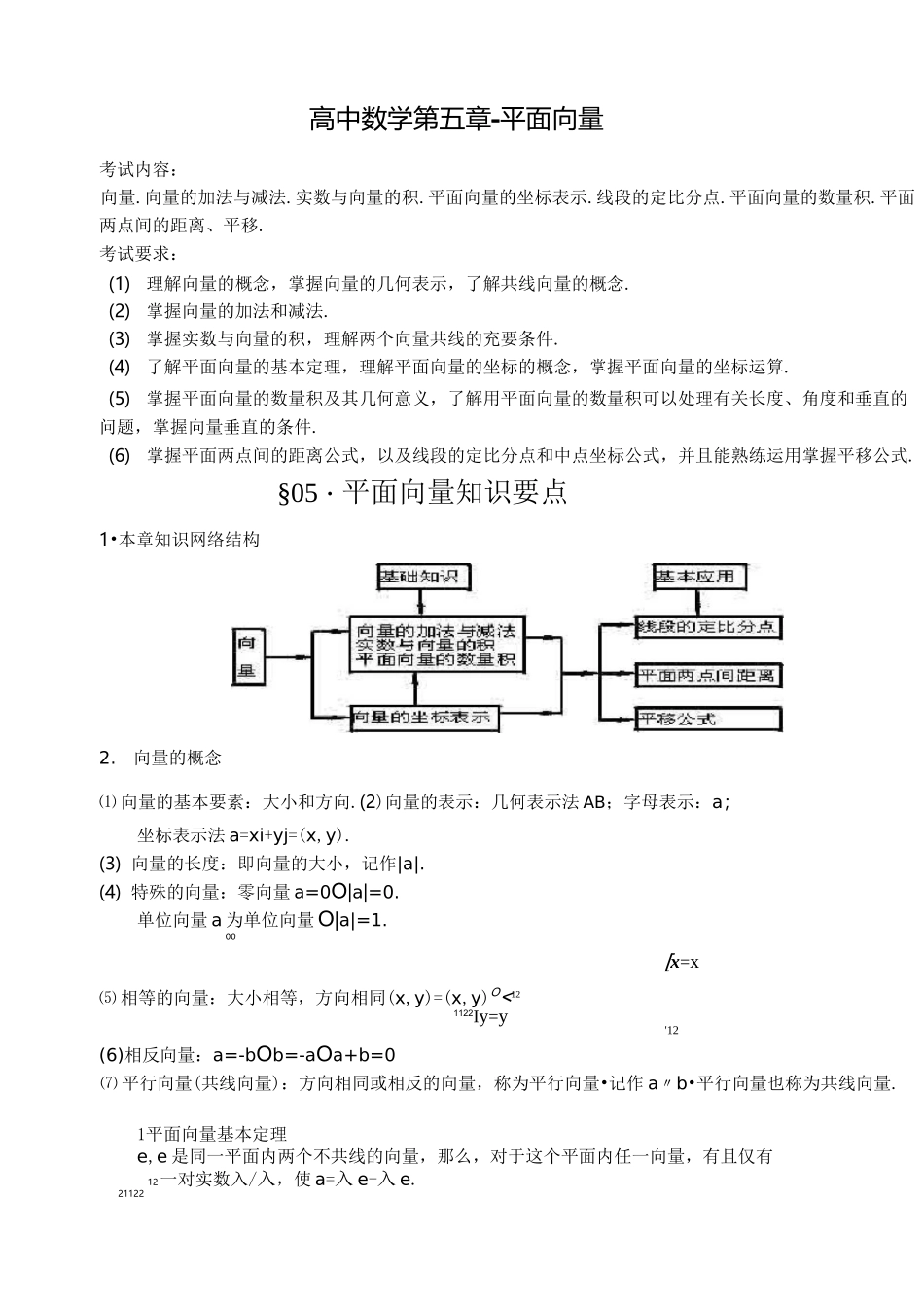
高中数学第五章-平面向量考试内容:向量.向量的加法与减法.实数与向量的积.平面向量的坐标表示.线段的定比分点.平面向量的数量积.平面两点间的距离、平移.考试要求:(1)理解向量的概念,掌握向量的几何表示,了解共线向量的概念.(2)掌握向量的加法和减法.(3)掌握实数与向量的积,理解两个向量共线的充要条件.(4)了解平面向量的基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算.(5)掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的条件.(6)掌握平面两点间的距离公式,以及线段的定比分点和中点坐标公式,并且能熟练运用掌握平移公式.§05・平面向量知识要点1•本章知识网络结构2.向量的概念⑴ 向量的基本要素:大小和方向.(2)向量的表示:几何表示法 AB;字母表示:a;坐标表示法 a=xi+yj=(x,y).(3) 向量的长度:即向量的大小,记作|a|.(4) 特殊的向量:零向量 a=0O|a|=0.单位向量 a 为单位向量 O|a|=1.00[x=x⑸ 相等的向量:大小相等,方向相同(x,y)=(x,y)O<121122Iy=y'12(6)相反向量:a=-bOb=-aOa+b=0⑺ 平行向量(共线向量):方向相同或相反的向量,称为平行向量•记作 a〃b•平行向量也称为共线向量.1平面向量基本定理e,e 是同一平面内两个不共线的向量,那么,对于这个平面内任一向量,有且仅有12一对实数入/入,使 a=入 e+入 e.211223.向量的运算运算类型几何方法坐标方法运算性质向量的加法1•平行四边形法则2.三角形法则a+b=(x+x,y+y)1212—►―►—►—>a+b=b+a—►—►—►—►—►—►(a+b)+c=a+(b+c)向量的减法三角形法则a—b=(x—x,y—y)1212—►—►—►―»a 一 b=a+(—b)AB=—BA,OB—OA=AB数乘向量1. 九 a 是一个向量,满足:i 九 ai=i 九 IIai2.九>0 时,九 a 与 a 同向;九〈0 时,九 a 与 a 异向;九 a=(九 x,九 y)—►—>九(pa)=(九卩)a(九+p)a=Xa+pa 九(a+b)=Xa+Xba//bOa=Xb向量a•b 是一个数—►—►—►—►a•b=b•a1.a=0 或 b=0 时,(Xa)•b=a•(Xb)=X(a•b)的数量积—►―►a•b=0.—>—>a•b=xx+yy1212—►—►—►—►—>—►—►(a+b)•c=a•c+b•ca 丰 0 且 b 丰 0 时,2.一一一一a・b=IaIIbIcos(a,b)a123=IaI2即 lal=Jx2+y2Ia•bivaIIbI4•重要定理、公式2两个向量平行的充要条件a〃bOa=入 b(b 工 0)Oxy—xy=O.12213两个向量垂直的充要条件a 丄 bOa•b=OOxx+yy=O.1212(线段定比分...