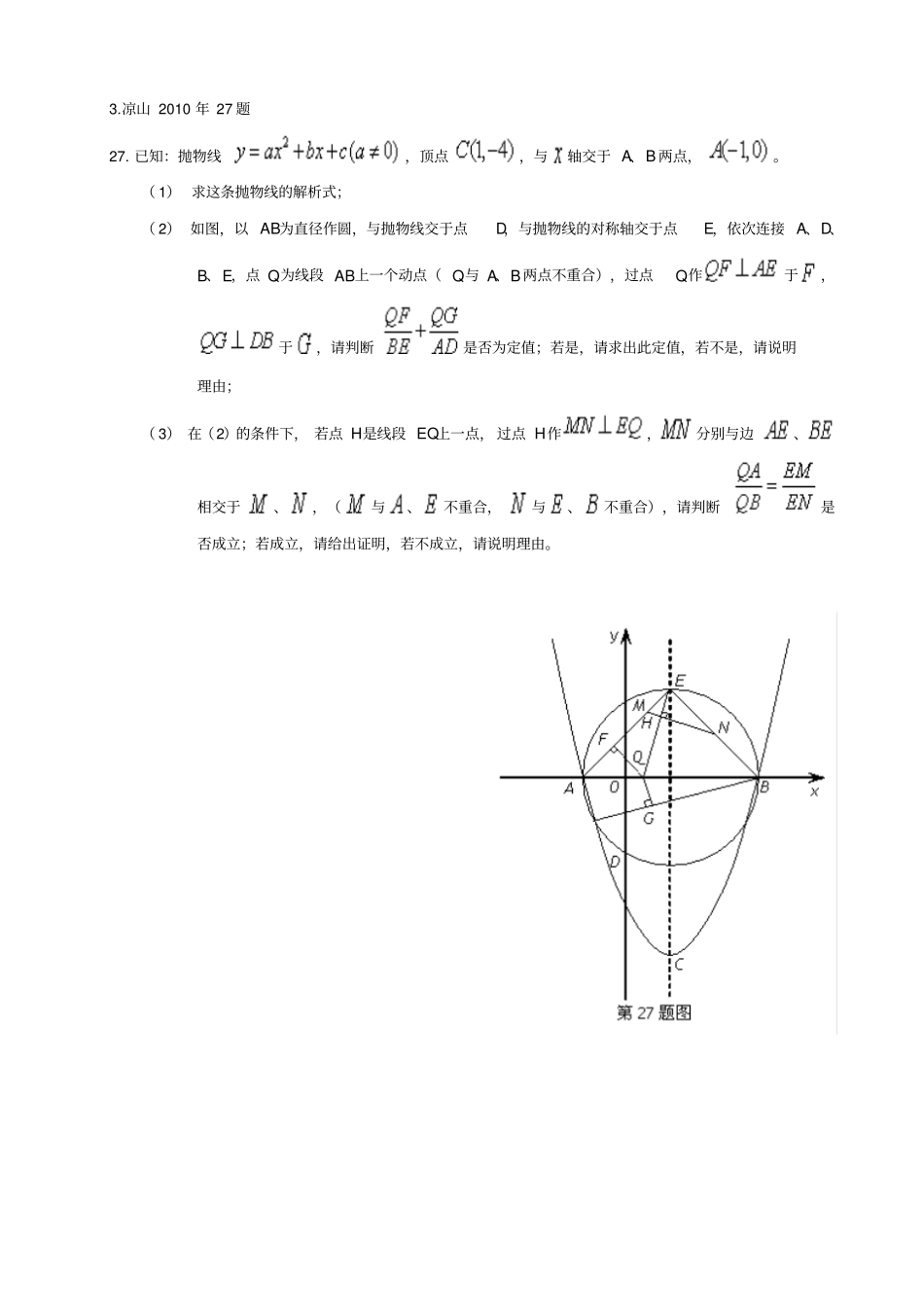
凉山州历年中考压轴题及参考答案1. 凉山 2008 年第 25 题25.(9 分)如图,在中,是的中点,以为直径的交的三边,交点分别是点.的交点为,且,.(1)求证:.(2)求的直径的长.(3)若,以为坐标原点,所在的直线分别为轴和轴,建立平面直角坐标系,求直线的函数表达式.2. 凉山 2009 年 26 题26.如图,已知抛物线经过,两点,顶点为.( 1)求抛物线的解析式;( 2)将绕点顺时针旋转90° 后,点落到点的位置,将抛物线沿轴平移后经过点,求平移后所得图象的函数关系式;(3)设( 2)中平移后,所得抛物线与轴的交点为,顶点为,若点在平移后的抛物线上,且满足的面积是面积的 2 倍,求点的坐标.3.凉山 2010 年 27 题27. 已知:抛物线,顶点,与轴交于 A、B 两点,。( 1) 求这条抛物线的解析式;( 2) 如图,以 AB为直径作圆,与抛物线交于点D,与抛物线的对称轴交于点E,依次连接 A、D、B、E,点 Q为线段 AB上一个动点( Q与 A、B 两点不重合),过点Q作于,于,请判断是否为定值;若是,请求出此定值,若不是,请说明理由;( 3) 在(2)的条件下, 若点 H是线段 EQ上一点, 过点 H作,分别与边、相交于、,(与、不重合,与、不重合),请判断是否成立;若成立,请给出证明,若不成立,请说明理由。4.凉山 2011 年 28 题28. 如图,抛物线与轴交于(,0)、(,0)两点,且,与轴交于点,其中是方程的两个根。(1)求抛物线的解析式;(2)点是线段上的一个动点, 过点作∥,交于点,连接,当的面积最大时,求点的坐标;( 3)点在( 1)中抛物线上,点为抛物线上一动点,在轴上是否存在点,使以为顶点的四边形是平行四边形,如果存在, 求出所有满足条件的点的坐标,若不存在,请说明理由。5.凉山 2012 年 28 题28.( 12 分)如图,在平面直角坐标系中,直线y=x+ 4 与 x 轴、 y 轴分别交于A、B 两点,抛物线y=-x2+bx+c 经过 A、 B 两点,并与x 轴交于另一点C(点 C 点 A 的右侧),点P 是抛物线上一动点.(1)求抛物线的解析式及点C 的坐标;(2)若点 P 在第二象限内,过点P 作 PD⊥轴于 D,交 AB 于点 E.当点 P 运动到什么位置时,线段PE 最长?此时PE 等于多少?(3)如果平行于x 轴的动直线l 与抛物线交于点Q,与直线 AB 交于点 N,点 M 为 OA 的中点, 那么是否存在这样的直线l,使得△ MON 是等腰三角形?若存在...