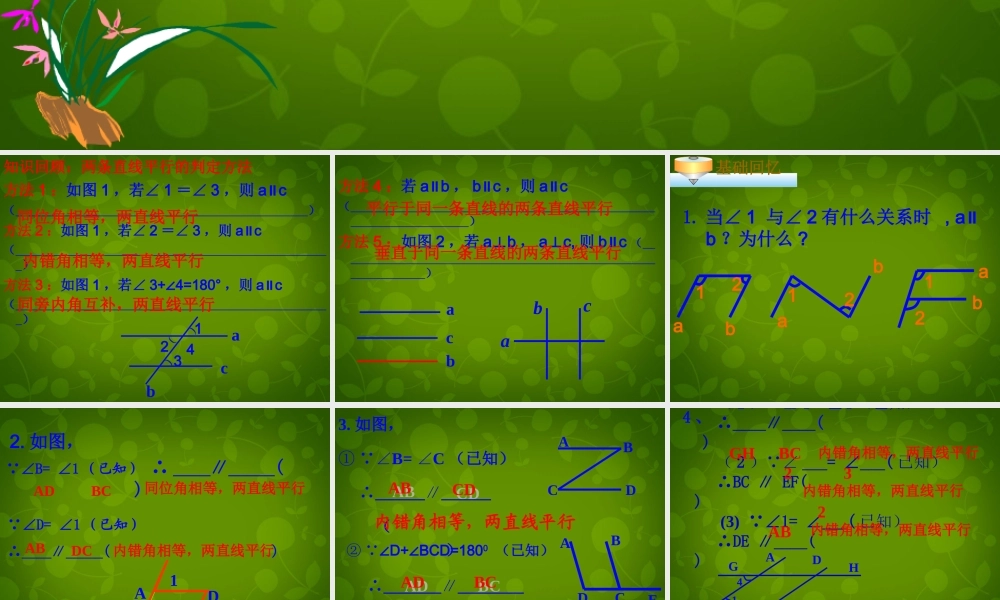
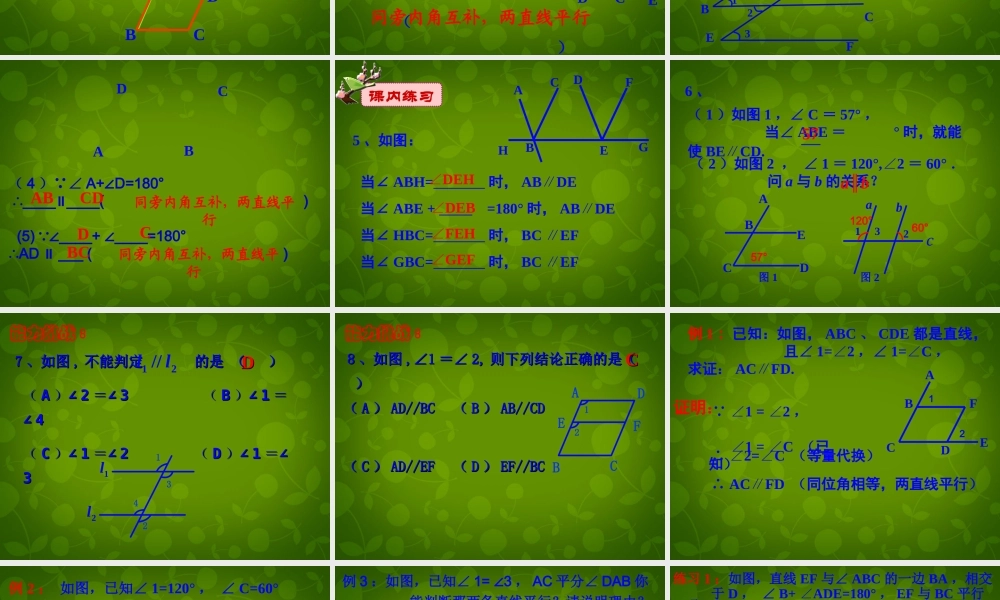
知识回顾:两条直线平行的判定方法方法 1 :如图 1 ,若∠ 1 =∠ 3 ,则 a c∥( )方法 2 :如图 1 ,若∠ 2 =∠ 3 ,则 a c∥( )方法 3 :如图 1 ,若∠ 3+ 4=180°∠,则 a c∥( )同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行abc)))1234方法 4 :若 a b∥ , b c∥ ,则 a c∥( )方法 5 :如图 2 ,若 ab⊥ , ac,⊥则 b c∥( )平行于同一条直线的两条直线平行 垂直于同一条直线的两条直线平行abcabc 1. 当∠ 1 与∠ 2 有什么关系时 , a∥b ?为什么 ? ababba121212基础回忆 ∠B= ∠1 (已知) ∴ ____∥_____( ) 1ABDC ∠D= ∠1 (已知)∴____∥_____( ) ADBC同位角相等,两直线平行ABDC内错角相等,两直线平行2. 如图,3. 如图, ① ∠B= C∠(已知) ∴____________∥ ( ) ② ∠D+ BCD=180∠0 (已知) ∴_______________∥ ( )内错角相等,两直线平行ABCDADBCEABABCDCDADADBCBC 同旁内角互补,两直线平行( 1 ) ∠ 1 =∠4 (已知)∴____∥____( )( 2 ) ∠ ___= ∠___( 已知)∴BC ∥ EF( ) (3) ∠1= ∠___( 已知)∴DE ∥____( )4 、 GCFEBHDA4123GHBC23内错角相等,两直线平行内错角相等,两直线平行2AB内错角相等,两直线平行( 4 ) ∠ A+ D=180°∠ ∴____ ____( )∥ (5) ____+ ____=180° ∠∠∴AD ___ ( )∥ADCBABCD 同旁内角互补,两直线平行DCBC 同旁内角互补,两直线平行ABCDEFGH5 、如图:当∠ ABH= 时, ABDE∥当∠ ABE + =180° 时, ABDE∥当∠ HBC= 时, BC EF∥当∠ GBC= 时, BC EF∥课内练习∠DEH∠DEB∠FEH∠GEF ( 1 )如图 1 ,∠ C = 57° , 当∠ ABE = ° 时,就能使 BE∥CD. ( 2 )如图 2 , ∠ 1 = 120°,2∠ = 60° . 问 a 与 b 的关系? 图 1图 2a∥b ABECD 5736 、57°12abc120°60°能力挑战 :(( AA∠)∠)22∠=∠=33 (( BB∠)∠)11 ==∠∠ 44 (( CC∠)∠)11∠=∠=22 (( DD∠)∠)11∠=∠=33 DD77 、如图、如图 ,, 不能判定 的是 ( )不能判定 的是 ( )12//ll13241l2l能力挑战 :88 、如图、如图 ,∠1,∠1 =∠=∠ 2,2, 则下列结论正确的是( 则下列结论正确的是( ) )ABCDEF12(( AA...