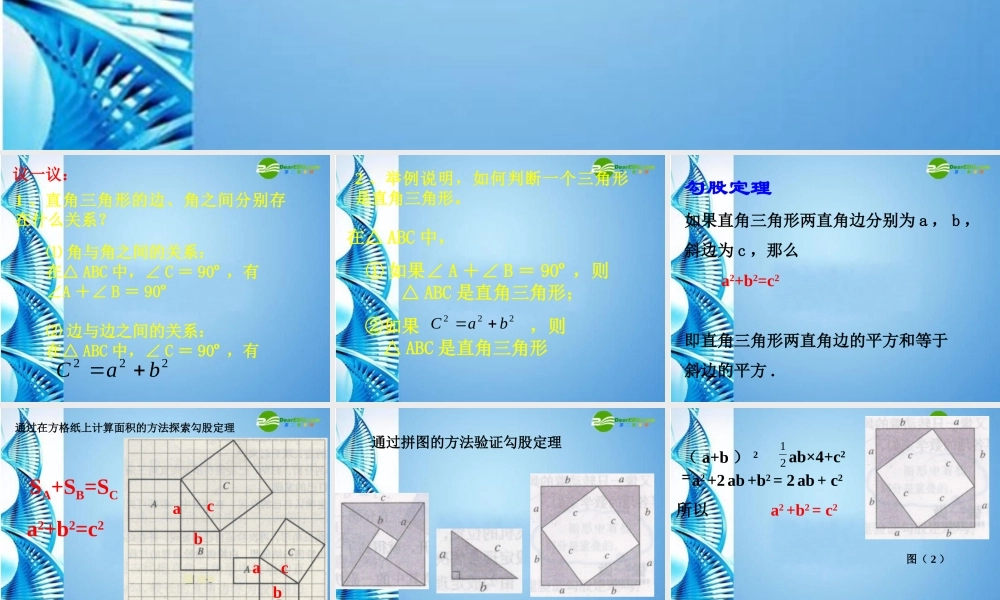
第一章勾股定理 回顾与思考1 、直角三角形的边、角之间分别存在什么关系?⑴ 角与角之间的关系:在△ ABC 中,∠ C = 90º ,有∠A +∠ B = 90º⑵ 边与边之间的关系:在△ ABC 中,∠ C = 90º ,有222baC议一议:2 、举例说明,如何判断一个三角形是直角三角形。在△ ABC 中, ① 如果∠ A +∠ B = 90º ,则 △ ABC 是直角三角形; ②如果 ,则 △ ABC 是直角三角形 222baC勾股定理如果直角三角形两直角边分别为 a , b ,斜边为 c ,那么 a2+b2=c2即直角三角形两直角边的平方和等于斜边的平方 .通过在方格纸上计算面积的方法探索勾股定理abcabcSA+SB=SCa2+b2=c2图( 1 )图( 2 )通过拼图的方法验证勾股定理图( 2 )ab×4+c221( a+b ) 2 =a2 +2 ab +b2 = 2 ab + c2所以 a2 +b2 = c2 如果三角形的三边长 a , b , c 满足 a2 +b2 = c2 ,那么这个三角形是直角三角形 . 满足 a2 +b2 = c2 的三个正整数,称为勾股数 .1.下列几组数能否作为直角三角形的三边长? 说说你的理由 . ( 1 ) 9 , 12 , 15 ( ) ( 2 ) 15 , 36 , 39 ( ) ( 3 ) 12 , 18 , 22 ( ) 2. 如图,正方形网格中的△ ABC ,若小方格边长为 1 ,则△ ABC 是( )( A )直角三角形 (B) 锐角三角形 (C) 钝角三角形 (D) 以上答案都不对 ABC3. 在△ ABC 中, AB=13 , AC=20 ,高AD=12 , 则 BC 的长为————————————————CA20B13D┓12165AC20B13D┓1251621 或 114. 如图,有一个长方体的长、宽、高分别是 6 、 4 、4 , 在底面 A 处有一只蚂蚁,它想吃到长方体上面与 A 相对的 B 点处的食物,需要爬行的最短路程是 ________.105. 小明家住在 18 层的高楼上 . 一天 , 他与妈妈去买竹竿 . 如果电梯的长、宽、高分别是 1.5 、 1.5 、2.2 米,那么能放入电梯内的竹竿的最大长度大约是多少?你能估计出小明买的竹竿至少是多少米吗?解:∵∠ ADB=90° ∴AB2=AD2+BD2 =1.52+1.52 = 4.5 ∵∠ABC=90° ∴AC2=AB2+BC2 =4.5+2.22 =9.34 而 3.12=9.61所以能放入电梯内的竹竿的最大长度大约是 3 米,小明买的竹竿至少是 3.1 米 .ABCD 课 堂 小 结1 、勾股定理:2 、直角三角形的判别条件。3 、在本章中所体现的数学思想方法是数形结合思想。4 、本章知识结构图5 、了解了勾股定理的历史四、作业1 、课本第 16 页复习题A 组 1 , 2 , 3 , 4 , 5 B 组 12 、独立完成一份小结,用自己的语言梳理本章的内容。 3 、复习本章知识点。