微积分基本定理(1) 高二数学微积分基本定理课件新课标选修2 高二数学微积分基本定理课件新课标选修2VIP免费

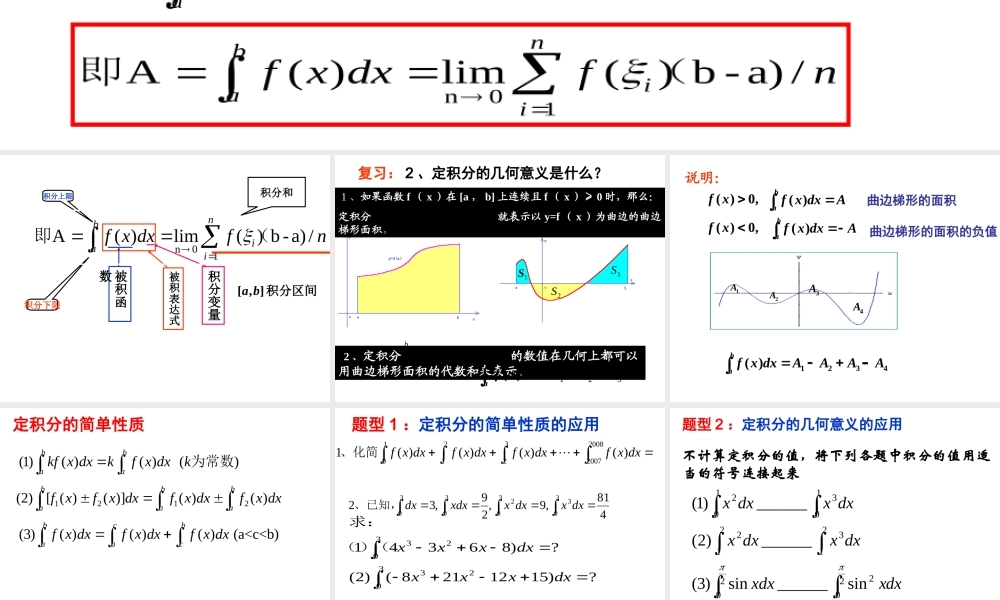
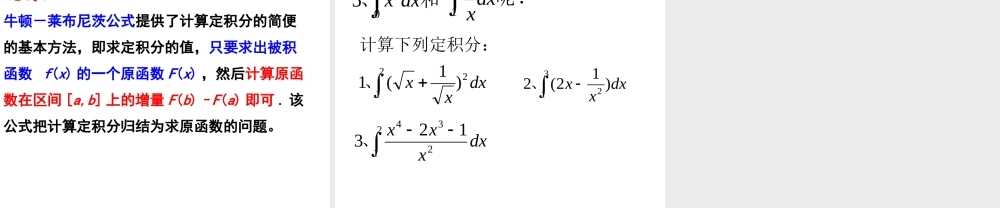bxxxxxann1210],[ 1iiixx 任取niixf1)(做和式：常数）且有，(/))((lim10Anabfniin复习： 1 、定积分是怎样定义？设函数 f （ x ）在 [a ， b] 上连续，在 [a ， b] 中任意插入 n-1个分点：把区间 [a,b] 等分成 n 个小区间，],[ 1iixx 在每个小区间./))((1nabfniibadxxf)(则，这个常数 A 称为 f(x) 在 [a ， b] 上的定积分 ( 简称积分 )记作nfdxxfniiba/a)-b)(lim)(A10n（即xfSii)( 被积函数被积表达式积分变量积分区间],[ba积分上限积分下限nfdxxfniiba/a)-b)(lim)(A10n（即积分和 1 、如果函数 f （ x ）在 [a ， b] 上连续且 f （ x ）≥ 0 时，那么：定积分 就表示以 y=f （ x ）为曲边的曲边梯形面积。badxxf)( 2 、定积分 的数值在几何上都可以用曲边梯形面积的代数和来表示。badxxf)(1S2S3S321SSSdxxfba)(复习： 2 、定积分的几何意义是什么？ ,0)(xfbaAdxxf)(曲边梯形的面积,0)(xfbaAdxxf)(曲边梯形的面积的负值4321)(AAAAdxxfba说明：1A2A3A4A 定积分的简单性质(1)( )( ) ()bbaakf x dxkf x dxk为常数1212(2)[ ( )( )]( )( )bbbaaaf xfx dxf x dxfx dx(3)( )( )( ) (a