人教版高一数学正弦余弦函数的图象和性质 奇偶性及对称性 课件VIP免费

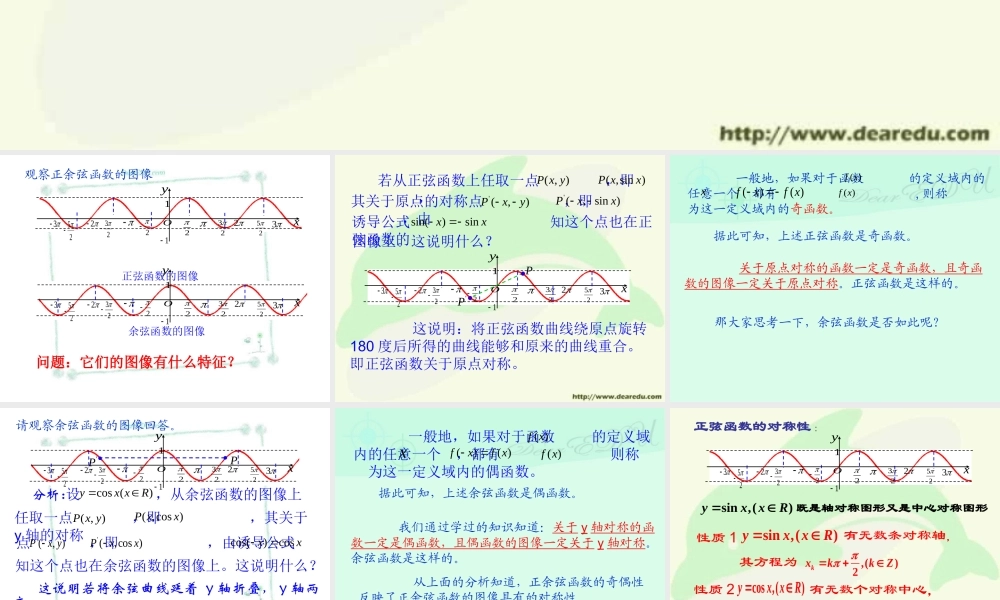
问题：它们的图像有什么特征？观察正余弦函数的图像x22322523yO23225311正弦函数的图像余弦函数的图像x22322523yO23225311x22322523yO23225311 若从正弦函数上任取一点 ，即 ， ),(yxP( ,sin )P xx其关于原点的对称点 ，即 ，由'(,)Pxy'(, sin )Pxx诱导公式 知这个点也在正弦函数的xxsin)sin(图像上。这说明什么？P'P 这说明：将正弦函数曲线绕原点旋转180 度后所得的曲线能够和原来的曲线重合。即正弦函数关于原点对称。 一般地，如果对于函数 的定义域内的任意一个 都有 , 则称 为这一定义域内的奇函数。)(xfx)()(xfxf)(xf据此可知，上述正弦函数是奇函数。 关于原点对称的函数一定是奇函数，且奇函数的图像一定关于原点对称。正弦函数是这样的。那大家思考一下，余弦函数是否如此呢？点 ，即 ，由诱导公式'(, )Px y'(,cos )Pxxxxcos)cos(任取一点 ，即 ，其关于y 轴的对称),(yxP( ,cos )P xx请观察余弦函数的图像回答。分析：设)(cosRxxy，从余弦函数的图像上知这个点也在余弦函数的图像上。这说明什么？'PPx22322523yO23225311 这说明若将余弦曲线延着 y 轴折叠， y 轴两旁的部分能够互相重合 ，即余弦曲线关于 y 轴对称。 我们通过学过的知识知道：关于 y 轴对称的函数一定是偶函数，且偶函数的图像一定关于 y 轴对称。余弦函数是这样的。 从上面的分析知道，正余弦函数的奇偶性反映了正余弦函数的图像具有的对称性。 一般地，如果对于函数 的定义域内的任意一个 ，都有 则称 为这一定义域内的偶函数。)(xfx()( )fxf x)(xf据此可知，上述余弦函数是偶函数。正弦函数的对称性 :既是轴对称图形又是中心对称图形sin ,()yxxR性质 1有无数条对称轴，sin ,()yxxR,()2kxkkZ其方程为性质 2有无数个对称中心，cos ,()yx xR(,0),()kkZ其坐标为x22322523yO23225311余弦函数的对称性 :既是轴对称图形又是中心对称图形)(,cosRxxy性质 1有无数条对称轴，cos ,()yxxR,()2kxkkZ其方程为性质 2有无数个对称中心，cos ,()yxxR(,0),()2kkZ 其坐标为余弦函数的图像x22322...