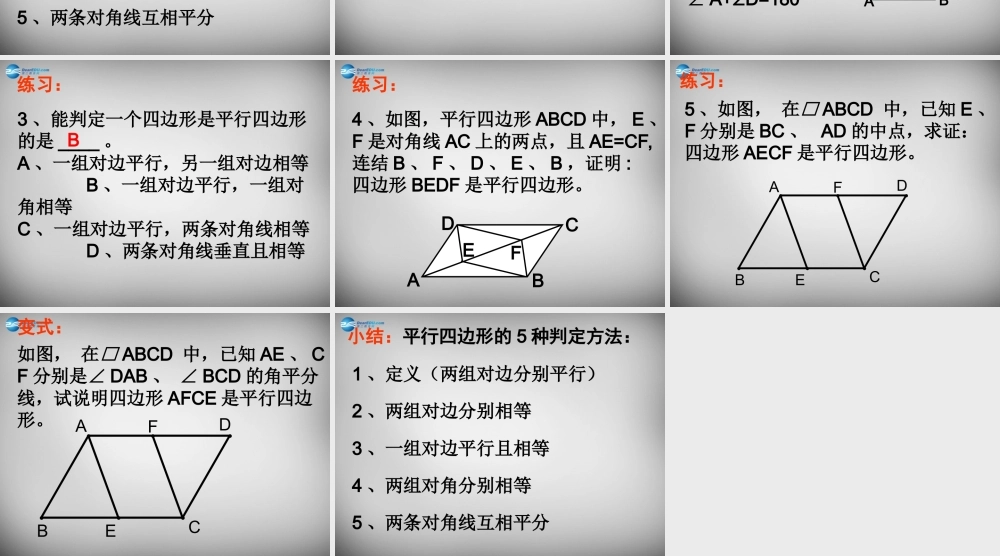
平行四边形的判定 1温故知新:1 、平行四边形的定义?2 、平行四边形的性质?猜想与探究:平行四边形性质的逆命题成立吗?探究:如图,四边形 ABCD 满足以下条件,能否证明它是平行四边形? ① AB=CD , AD=BC ③ ∠A= C∠,∠ B= D∠ABCD ② AB CD∥, AB=CD ④ AO=CO , BO=DO 探究:四边形 ABCD 的对角线交于 O ,满足以下条件,能否证明是平行四边形?ABCDO1 、两组对边分别平行(定义)2 、两组对边分别相等平行四边形的判定方法:3 、一组对边平行且相等4 、两组对角分别相等5 、两条对角线互相平分练习:1 、不能判定四边形 ABCD 为平行四边形的条件是 ( )A 、 AB CD∥且 AB=CD B 、 AB=CD , AD=BCC 、 AB CD∥且 AB=BC D 、 AB//CD , BC//ADCABCD练习:2 、四边形 ABCD 中 , AD BC∥,要判定 ABCD 是平行四边形,那么还需满足( )A 、∠ A+ C=180° B∠、∠ B+ D=180°∠C 、∠ A+ B=180° D∠、∠ A+ D=180°∠DABCD练习:3 、能判定一个四边形是平行四边形的是 ____ 。A 、一组对边平行,另一组对边相等 B 、一组对边平行,一组对角相等C 、一组对边平行,两条对角线相等 D 、两条对角线垂直且相等B练习:4 、如图,平行四边形 ABCD 中, E 、F 是对角线 AC 上的两点,且 AE=CF,连结 B 、 F 、 D 、 E 、 B ,证明 :四边形 BEDF 是平行四边形。ABCDEF练习:FDABCE5 、如图, 在□ ABCD 中,已知 E 、F 分别是 BC 、 AD 的中点,求证:四边形 AECF 是平行四边形。变式:FDABCE如图, 在□ ABCD 中,已知 AE 、 CF 分别是∠ DAB 、 ∠ BCD 的角平分线,试说明四边形 AFCE 是平行四边形。1 、定义(两组对边分别平行)2 、两组对边分别相等小结:平行四边形的 5 种判定方法:3 、一组对边平行且相等4 、两组对角分别相等5 、两条对角线互相平分