广东省高三数学 第9章第4节 空间向量课件 理 课件VIP免费

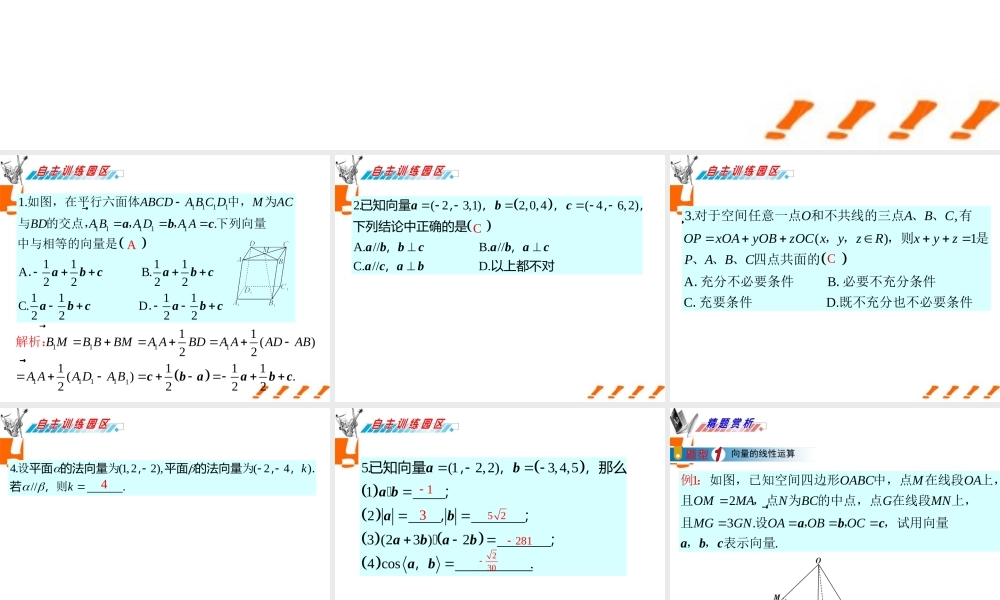
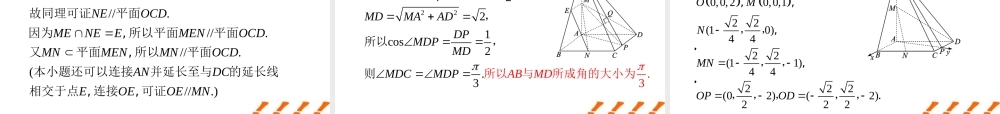1111111111.. 1111A B.22221111C. D2222ABCDA B C DMACBDA BA DA Aabcabcabcabcabc� 如图，在平行六面体中，为与的交点，，，下列向量中与相等的向量是．．A11111111111 ()221111().2222B MB BBMA ABDA AADABA AA DA B cbaabc��解析：2.( 23,1)2,0,4( 46,2) A. // B. //C. // D.  已知向量，,,，,下列结论中正确的是，，，以上都不对abca bbca baca cabC3.,()1 ABCD.OABCOPxOAyOBzOC xyzRxyzPABC� 对于空间任意一点 和不共线的三点 、 、有， ，，则是、 、 、 四点共面的. 充分不必要条件 . 必要不充分条件. 充要条件 既不充分也不必要条件C4.(1,22),( 24)// .kk 设为为则平面 的法向量，平面 的法向量， ， ．若， 4    5.(12,2)3,4,51 2 3 (23 )2 4 cos . 已知向量，，，那么； ，；；，aba babababab135 2 281230向量的线性运算213..OABCMOAOMMANBCGMNMGGNOAOBOCabcabc�如图，已知空间四边形中，点在线段上，且，点 为的中点，点 在线段上，且设，，，试用向量， ，例表示向量：233423 ()3423 12[ ()]34 23231133 .382688OGOMMGOAMNOAONOMOAOBOCOAabcaabc���解析：1.2.1 ().2BACOBOAOC�本题主要考查用基向量表示空间图形中指定的向量. 解题的基本思路是结合图形特点运用向量的三角形法则或平行四边形法则、共线向量定理等基本关系表示出有关的向量．向量的线性运算有一个常用的结论：如反思小结：果点 是点 、连线段的中点，则有常用于与中点相关的运算． .GABCOOAOBOCOG�已知点 是的重心,是空间任意一点．若拓展练习1：，则 的值是 333.23BCDOAODOAOBOCOG��设的中点为 ，，解故则析：向量的坐标运算11111112ABCDA B C DMNBBC DAMN已知正方体中,、 分别为、的中点. 建立适当的坐标系，求平面例 ：的法向量．1DDADCDDxyz以 为原点，、、所在直线分别为 轴、 轴、轴建立空间直角坐标系, 如解析：图所示．11111111,0,0(1,1)(01)2211(0,1)( 11)22()102.102234( 3,24)( 3,24)ABCDA B C DAMNAMANAMNxyzAMyzANxyzyxzAM ...