八年级数学下册 9.2 30°、45°、60°角的三角比课件 青岛版 课件VIP免费

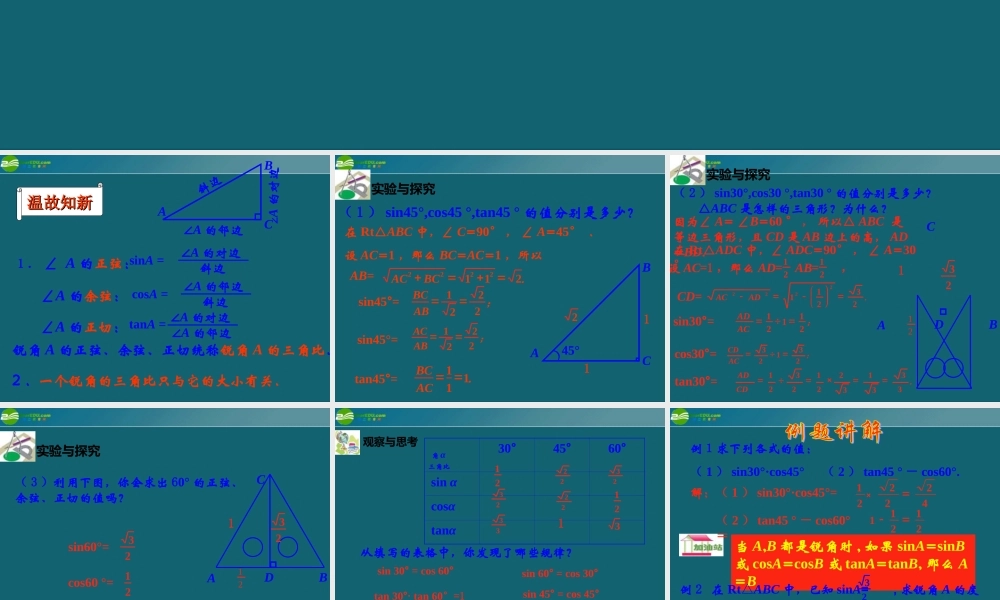
温故知新温故知新1 ． ∠ A 的正弦：sinA =∠A 的对边斜边∠A 的余弦： cosA =∠A 的邻边斜边∠A 的正切：tanA = ∠A 的对边∠A 的邻边锐角 A 的正弦、余弦、正切统称锐角 A 的三角比．2 ．一个锐角的三角比只与它的大小有关．ABC斜边∠A 的邻边∠A 的对边实验与探究（ 1 ） sin45°,cos45 °,tan45 ° 的值分别是多少？ABC（45°在 Rt△ABC 中，∠ C=90° ， ∠ A=45° ．设 AC=1 ，那么 BC=AC=1 ，所以112AB=．BCAC2112222sin45°=；ABBC2221 sin45°=；ABAC2221 tan45°=．ACBC111实验与探究（ 2 ） sin30°,cos30 °,tan30 ° 的值分别是多少？在 Rt△ADC 中，∠ ADC=90° ， ∠ A=30°1CABD△ABC 是怎样的三角形？为什么？因为∠ A= ∠B=60 ° ， 所以△ ABC 是等边三角形，且 CD 是 AB 边上的高， AD=BD.设 AC=1 ，那么 AD= AB= ，2121CD=．ADAC232112222sin30°=；ACAD211212123cos30°=；ACCD23123tan30°=．CDAD333132212321×1CABD实验与探究（ 3 ）利用下图，你会求出 60° 的正弦、余弦、正切的值吗？sin60°=23cos60 °=21tan60 °=32123观察与思考 角 α三角比30°45°60° sin α cosα tanα1从填写的表格中，你发现了哪些规律？sin 30° = cos 60°sin 60° = cos 30°tan 30°· tan 60°=1 sin 45° = cos 45°如果∠ A ＋ ∠ B=90 ° ，那么 sin A = cosB , cos A = sinB ．212223321232233例１求下列各式的值：（ 1 ） sin30°·cos45°（ 2 ） tan45 ° － cos60°.当 A,B 都是锐角时 , 如果 sinA=sinB或 cosA=cosB 或 tanA=tanB, 那么 A=B解：（ 1 ） sin30°·cos45°=422221×（ 2 ） tan45 ° － cos60°＝21211例 2 在 Rt△ABC 中，已知 sinA= , 求锐角 A 的度数．23解：因为 A 是锐角，并且 sinA ＝ ，由于 sin60 °= ,所以∠ A= 60 ° ．2323如图，作边长为 1 的正方形 ABCD ．延长边 CB 到 D ′ ，使 B D ′ ＝ B D ，连接 D D ′ ．你能利用这个图形求出 22 . 5° 角的正切的值吗？试一试．ABCDD′tan22.5 °=12 （ 1 ） sin30° － cos30°=________; （ 2 ） ·tan60 °=_____.（ 1 ） sin30° ＋ cos60°; （ 2 ） tan30 °· tan60 °;（ 3 ） 2sin60° － tan30 °; （ 4 ） sin45°· cos45° ＋ tan45 ° ．2. 求下列各式的值：１ . 求下列各式的值：2323231 （ 4 ） ． 23（ 1 ） 1;（ 2 ） 1;332（ 3 ） ;如果∠ A ＋ ∠ B=90 ° ，那么 sin A = cosB , cos A = sinB ．1. 特殊角的三角函数．2. 已知特殊三角函数值，会求特殊角． 角 α三角比30°45°60° sin α cosα tanα1212223321232233必做题 : 课本 P68A 组 1 、 2 题选做题 : 课本 P68B 组 1 、 2 、 3 、 4题同学们 ,再见 !