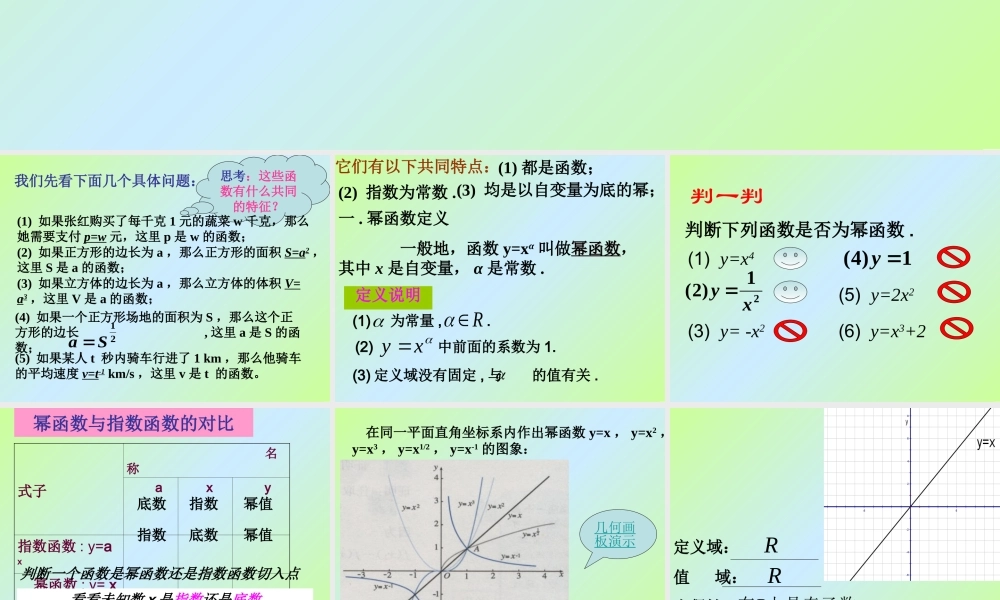
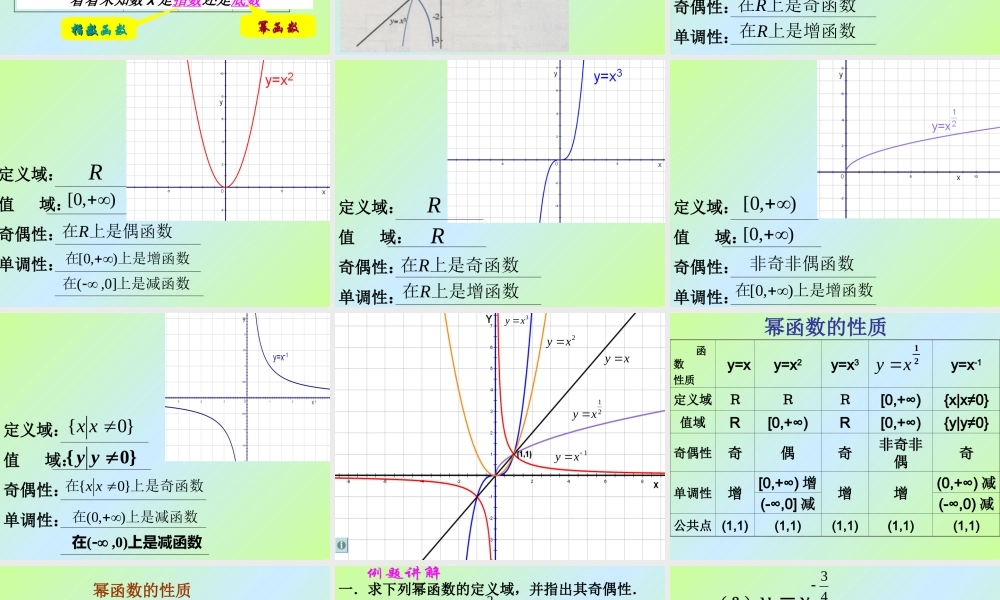
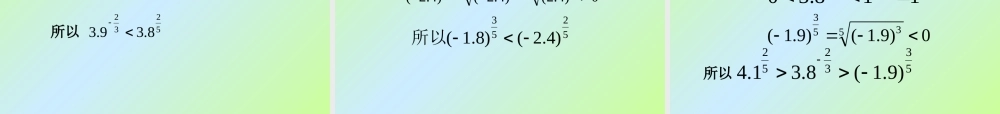思考:这些函数有什么共同的特征?我们先看下面几个具体问题:(1) 如果张红购买了每千克 1 元的蔬菜 w 千克,那么她需要支付 p=w 元,这里 p 是 w 的函数;(2) 如果正方形的边长为 a ,那么正方形的面积 S=a2 ,这里 S 是 a 的函数;(3) 如果立方体的边长为 a ,那么立方体的体积 V=a3 ,这里 V 是 a 的函数;(5) 如果某人 t 秒内骑车行进了 1 km ,那么他骑车的平均速度 v=t-1 km/s ,这里 v 是 t 的函数。(4) 如果一个正方形场地的面积为 S ,那么这个正方形的边长 , 这里 a 是 S 的函数;21Sa 它们有以下共同特点:(1) 都是函数;(3) 均是以自变量为底的幂;(2) 指数为常数 .一 . 幂函数定义 一般地,函数 y=xα 叫做幂函数幂函数,其中 x 是自变量, α 是常数 .(1) 为常量 , .定义说明(2) 中前面的系数为 1.(3) 定义域没有固定 , 与 的值有关 .Rxy 判断下列函数是否为幂函数 .(1) y=x4 21)2(xy (3) y= -x2 1)4(y(5) y=2x2 (6) y=x3+2 判一判 式子 名称 a x y指数函数 : y=a x 幂函数 : y= x a 底数指数指数底数幂值幂值幂函数与指数函数的对比判断一个函数是幂函数还是指数函数切入点看看未知数 x 是指数还是底数幂函数指数指数函数 在同一平面直角坐标系内作出幂函数 y=x , y=x2 ,y=x3 , y=x1/2 , y=x-1 的图象:几何画板演示 定义域:值 域:奇偶性:单调性:RR上是奇函数在R上是增函数在R 定义域:值 域:奇偶性:单调性:R),0[ 上是偶函数在R上是增函数在),0[ 上是减函数在]0,( 定义域:值 域:奇偶性:单调性:RR上是奇函数在R上是增函数在R 定义域:值 域:奇偶性:单调性:),0[ 非奇非偶函数上是增函数在),0[ ),0[ 定义域:值 域:奇偶性:单调性:}0{xx上是奇函数在}0{xx上是减函数在),0( 上是减函数在)0,(}0{yy 2xy xy 3xy 1xy21xy 函数性质 y=xy=x2y=x3y=x-1定义域RRR[0,+∞){x|x≠0}值域R[0,+∞)R[0,+∞){y|y≠0}奇偶性奇偶奇非奇非偶奇单调性增[0,+∞) 增增增(0,+∞) 减(-∞,0] 减(-∞,0) 减公共点 (1,1)(1,1)(1,1)(1,1)(1,1)幂函数的性质21xy (1) 所有的幂函数在 (0,+∞) 都有定义,并且图象都通过点 (1,1); (2) 如果 α >0,则幂函数图象过原点,并且在区间 [0,+∞) 上...