数学 2.2.2向量的减法课件 北师大版必修4 课件VIP免费

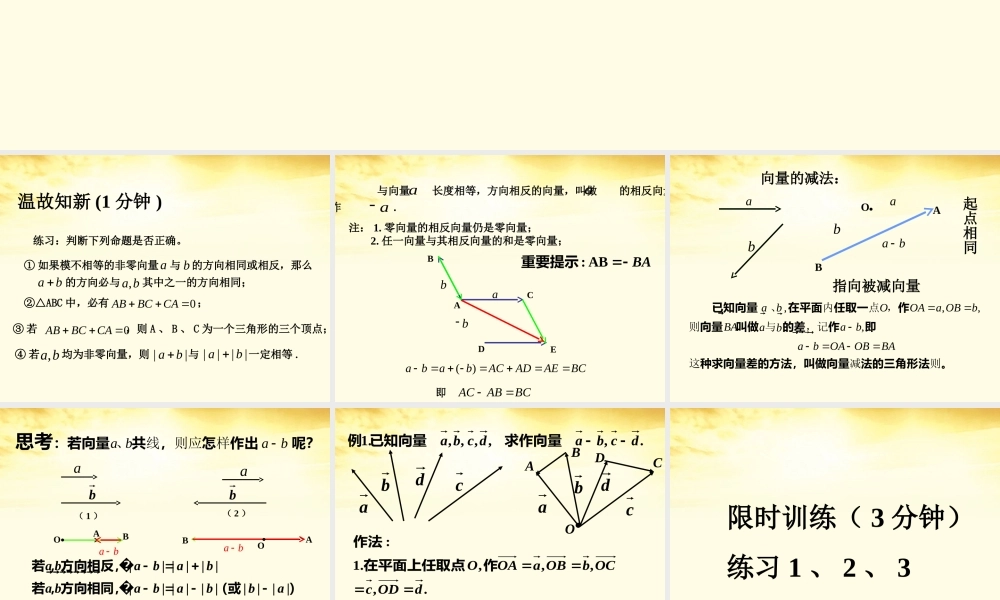
2.2.2 向量的减法练习：判断下列命题是否正确。① 如果模不相等的非零向量 与 的方向相同或相反，那么 的方向必与 其中之一的方向相同； abab,a b②△ABC 中，必有 ；0ABBCCA�③ 若 ，则 A 、 B 、 C 为一个三角形的三个顶点；0ABBCCA�④ 若 均为非零向量，则 与 一定相等 .,a b||ab||||ab温故知新 (1 分钟 ) 与向量 长度相等，方向相反的向量，叫做 的相反向量，记作 .aaa 注： 1. 零向量的相反向量仍是零向量； 2. 任一向量与其相反向量的和是零向量；ABCabDb E()ababACADAEBC  ��ACABBC�即: ABBA重要提示�abOBAabab向量的减法： ,,,,abOOAa OBbBAabababOAOBBA����� 、内点 ，则与，记 这减则 已知向量在平面任取一作 向量叫做的差作即种求向量差的方法，叫做向量法的三角形法。起点相同指向被减向量 a bab、线则应样 ：若向量共，怎作出呢？思考abab（ 1 ）（ 2 ）OABABOabab|| |||||| ||||||||a bababa bababba若 ，方向相反，若 ，方向相同，（或）|| ||||a babab若 ，不共线，则|||||| ||||a bababab对任意两个向量 ，，有||.,,,,,.1dcbadcba求作向量已知向量例ababccddABCDO.,,,.2.,,,,.1:为所求则作作在平面上任取点作法dcDCbaBADCBAdODcOCbOBaOAO限时训练（ 3 分钟）练习 1 、 2 、 3DBACbabADaABABCD,,,,,.2表示向量用已知平行四边形例abABCD解：有向量加法的平行四边形法则， 得ACab �;由向量的减法可得，.DBABADab �练习 . 化简：()()ABCDACBD�: ABBA重要提示�