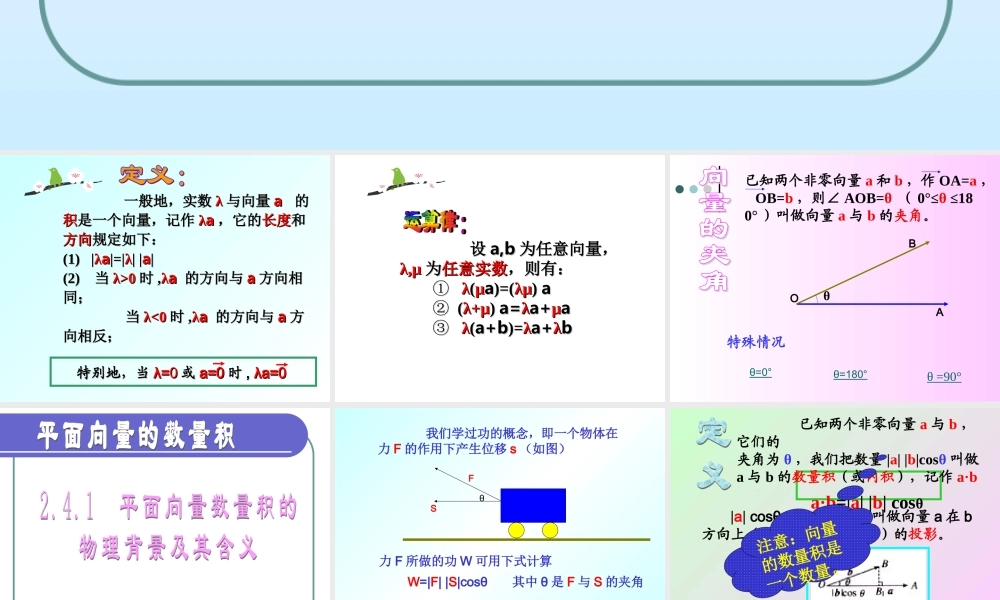
2.4.1 平面向量数量积的物理背景及其含义2.4.2 平面向量数量积的坐标表示、模、夹角 一般地,实数一般地,实数 λλ 与向量与向量 aa 的的积积是一个是一个向量向量,记作,记作 λλaa ,它的,它的长度长度和和方向方向规定如下:规定如下:(1) |(1) |λλaa|=||=|λλ| || |aa||(2) (2) 当当 λ>0λ>0 时时 ,,λλaa 的方向与的方向与 aa 方向相方向相同;同; 当当 λ<0λ<0 时时 ,,λλaa 的方向与的方向与 aa 方方向相反; 向相反; 特别地,当特别地,当 λ=λ=00 或或 a=0a=0 时时 , , λa=0λa=0 设设 a,ba,b 为任意向量,为任意向量,λ,μλ,μ 为为任意实数任意实数,则有:,则有: ① ① λλ((μμaa)=()=(λμλμ)) aa ② ② ((λ+μλ+μ) ) a=a=λλa+a+μμaa ③ ③ λλ((a+ba+b)=)=λλa+a+λλbb θ=180°θ =90°已知两个非零向量 a 和 b ,作 OA=a , OB=b ,则∠ AOB=θ ( 0°≤θ ≤180° )叫做向量 a 与 b 的夹角。θ=0°特殊情况OBAθ 我们学过功的概念,即一个物体在力 F 的作用下产生位移 s (如图)θFS力 F 所做的功 W 可用下式计算 W=|F| |S|cosθ 其中 θ 是 F 与 S 的夹角 从力所做的功出发,我们引入向量“数量积”的概念。 已知两个非零向量 a 与 b ,它们的夹角为 θ ,我们把数量 |a| |b|cosθ 叫做a 与 b 的数量积(或内积),记作 a·b a·b=|a| |b| cosθ规定 : 零向量与任一向量的数量积为 0 。 |a| cosθ ( |b| cosθ )叫做向量 a 在 b方向上(向量 b 在 a 方向上)的投影。注意:向量的数量积是一个数量。 向量的数量积是一个数量,那么它什么时候为正,什么时候为负?a·b=|a| |b| cosθ当 0°≤θ < 90° 时 a·b 为正;当 90° < θ ≤180° 时 a·b 为负。当 θ =90° 时 a·b 为零。 设 a , b 都是非零向量, e 是与 b 方向相同的单位向量, θ 是 a 与 e 的夹角,则 ( 1 ) e·a=a·e = |a| cosθ( 5 ) |a·b|≤|a||b|a·b|a||b|( 4 ) cosθ=( 3 )当 a 与 b 同向时, a·b=|a||b|当 a 与 b 反向时, a·b= - |a| |b|特别地, a·a =|a|2 或 |a|=√a·a 。( 2 ) ab a·b=0⊥OABθ abB1a·b=|a| |b| cosθ 解: a·b = |a| |b|cosθ= 5×4×cos120° =5×4× ( -1/2 ) = - 10例 1 已知 |a|=5 , |b|=4 , a 与 b 的夹角 θ=120° ,求 a·b 。例 2 已知 a=(1,1),b=(2,0), 求 a·b 。解: |a| =√2, |b|=2, θ=45 ° ∴ a·b=|a| |b|cosθ= √2×2×cos45 ° = 2 数量积 a·b 等于 a 的长度 |a|与 b 在 a 的方向上的投影 |b|cosθ 的乘积。OABθ|b|cosθ abB1 已知△ ABC 的顶点 A ( 1 , 1 ),B ( 4 , 1 ), C ( 4 , 5 )。计算 cosA, cosB, cosc. 1 . a·b=|a| |b| cosθ2. 数量积几何意义3. 重要性质