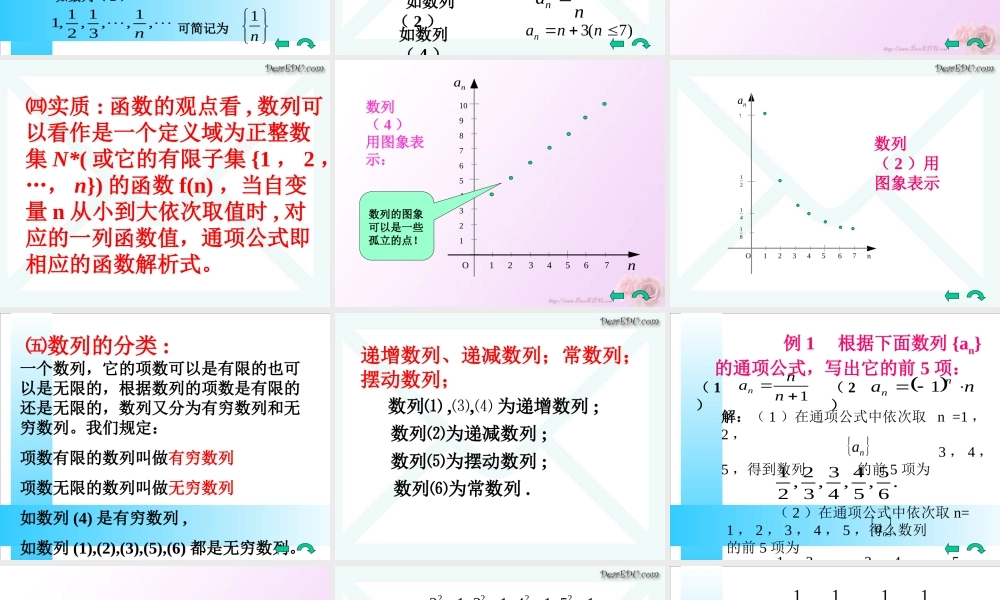
数列一-------- 数列、数列的通项公式 1 , 2 , 3 , 4 , 5 , ··· n , ··· . ( 1 ) 1 , , , , , ··· , ··· . ( 2 )n1213141511 , 1.4 , 1.41 , 1.414 , ··· . ( 3 ) 4 , 5 , 6 , 7 , 8 , 9 , 10. ( 4 )- 1 , 1 ,- 1 , 1 , ··· . ( 5 )1 , 1 , 1 , 1 , ··· . ( 6 )41421.12 ㈠数列的定义:㈠数列的定义: 按一定顺序排列的一列数叫数列。 按一定顺序排列的一列数叫数列。数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的第 1 项(首项),第 2 项, ······ ,第 n 项, ······ 。 注意: 根据数列的定义知数列是按一定顺序排列的一列数,因此若数列中被排列的数相同,但次序不同,则不是同一数列 .如: 数列( 4 ) 4 , 5 , 6 , 7 , 8 , 9 , 10.改为 数列( 4’ ) 10 , 9 , 8 , 7 , 6 , 5 ,4.它们不是同一数列 .又如:数列( 5 )- 1 , 1 ,- 1 , 1 , ···.改为 数列( 5’ ) 1 ,- 1 , 1 ,-1 , ···.则它们也不是同一数列 .㈡数列的一般形式可以写成:如数列( 2 ),1,,31,21,1n可简记为n1,,,,,321naaaa其中 是数列的第 n 项 , 上面的数列又可简记为 nana 如数列( 1 )1 , 2 , 3 , 4 , 5 , ··· ··· 可简记为 nnnan 如数列( 1 )nan1 如数列( 2 ))7(3nnan如数列( 4 )㈢数列的通项公式 如果数列 {an} 的第 n项 an 与 n 之间的函数关系可以用一个公式来表示,这个公式就叫做这个数列的通项公式 . 数列中的每一个数都对应着一个序号,反过来,每个序号也都对应着一个数 . 如数列( 4 )项 4 5 6 7 8 9 10序号 1 2 3 4 5 6 7 这说明:数列的项是序号的函数,序号从 1 开始依次增加时,对应的函数值按次序排出就是数列,这就是数列的实质。㈣实质 : 函数的观点看 , 数列可以看作是一个定义域为正整数集 N*( 或它的有限子集 {1 , 2 ,…, n}) 的函数 f(n) ,当自变量 n 从小到大依次取值时 , 对应的一列函数值,通项公式即相应的函数解析式。 O 1 2 3 4 5 6 710987654321nan数列( 4 ) 用图象表示:数列...