人教版高一数学正弦 余弦函数的性质 课件VIP免费

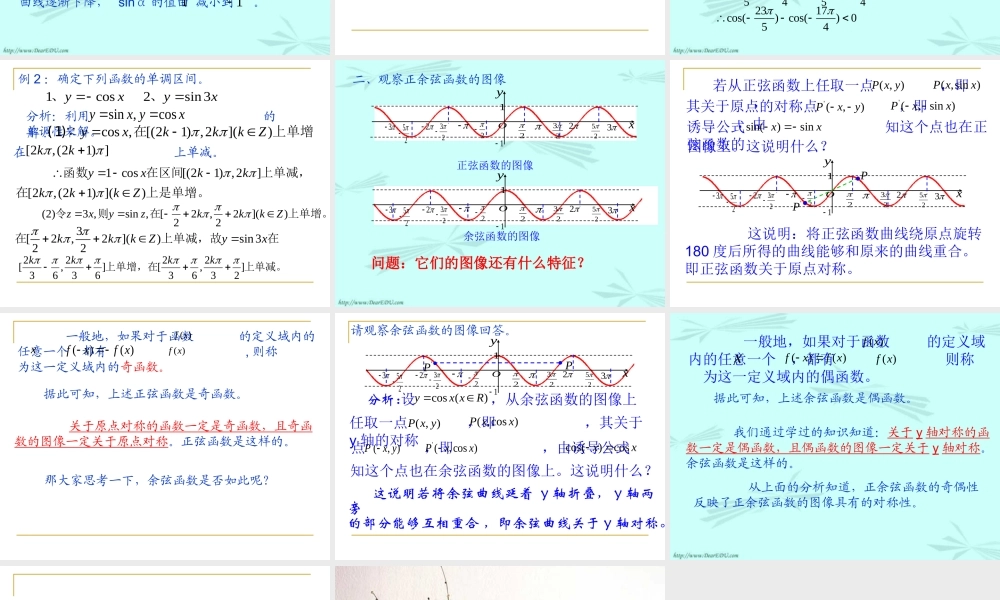
1 、 ，则 在 上是)()(21xfxf)(xfB单增函数；一、复习函数的单调性函数),)((Dxxfy若对于任意 ，12xxB、且 ，都有：21xx )(DB 单减函数；2 、 ，则 在 上是12( )()f xf x)(xfB函数的单调性反映了函数在一个区间上的走向。 请认真观察正余弦函数的图像，看看其是否具有这类性质？ 先看正弦函数图像从xysin的图像上可以看到函数具有什么特征？]2523[]22[]23,25[，、，、当 在区间…… 上时，x曲线逐渐上升， sinα 的值由 增大到 。11753357[,] [] [] [,]22222222…、，、 ，、…当 在区间x上时，曲线逐渐下降， sinα 的值由 减小到 。11x22322523yO23225311 由正弦函数的周期性知：正弦函数在每个闭区间)](22,22[Zkkk都是增函数，其值从－ 1 增大到 1 ；而在每个闭区间3[2,2]()22kkkZ上都是减函数，其值从 1 减小到－ 1 。 我们在来观察余弦函数的图像，看看是否有类似的特征。再来观察余弦函数图像从cosyx的图像上可以看到函数具有什么特征？[ 3 , 2 ] [0] [2 ][3 ,4 ]、 ，、 ，当 在区间x上时，曲线逐渐上升， cosα 的值由 增大到 。11曲线逐渐下降， sinα 的值由 减小到 。11[ 2 ,] [0] [23 ] 、，、 ，当 在区间x上时，x22322523yO23225311 由余弦函数的周期性知：其值从 1 减小到－ 1 。而在每个闭区间上都是减函数，])12(,2[kk其值从－ 1 增大到 1 ；在每个闭区间[(21) ,2]kk都是增函数， 当 x∈R 时，即在整个定义域内并不单调，图像时而上升，时而下降，存在规范的单调区间。由于它们是周期函数，因此在考虑函数增减的问题时，只要研究一个周期即可。分析：比较同名函数值的大小，往往可以利用函数的单调性，但需要考虑它是否在同一单调区间上，若是，即可判断，若不是，需化成同一单调区间后再作判断。0)10sin()18sin()18sin()10sin(即53cos523cos)523cos()2(、4cos417cos)417cos(例 1 ：不求值，判断下列各式的符号。)10sin()18sin(1、)417cos()523cos(2、解：上增函数。在且、]2,2[sin,2181021x...