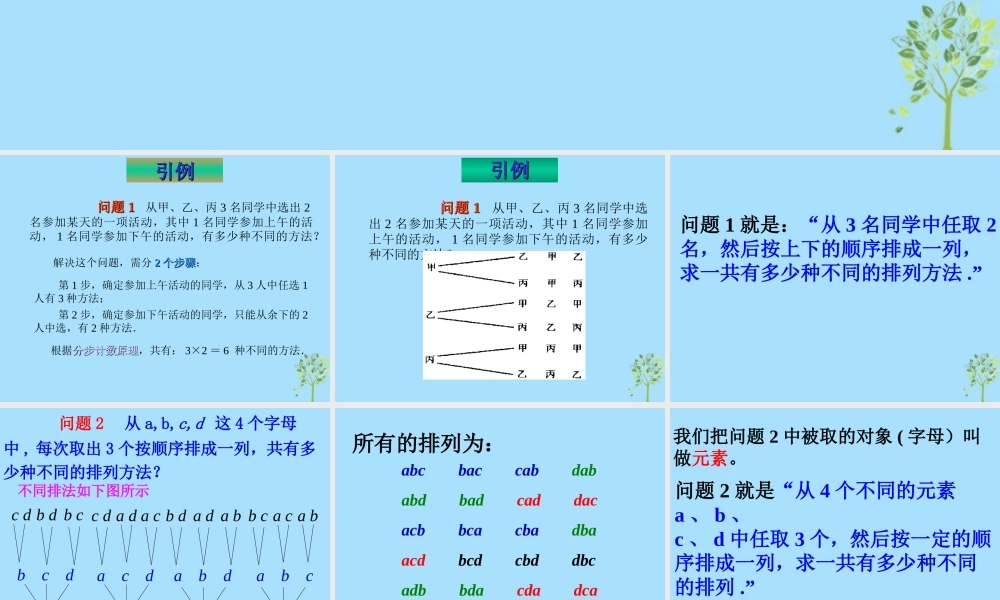
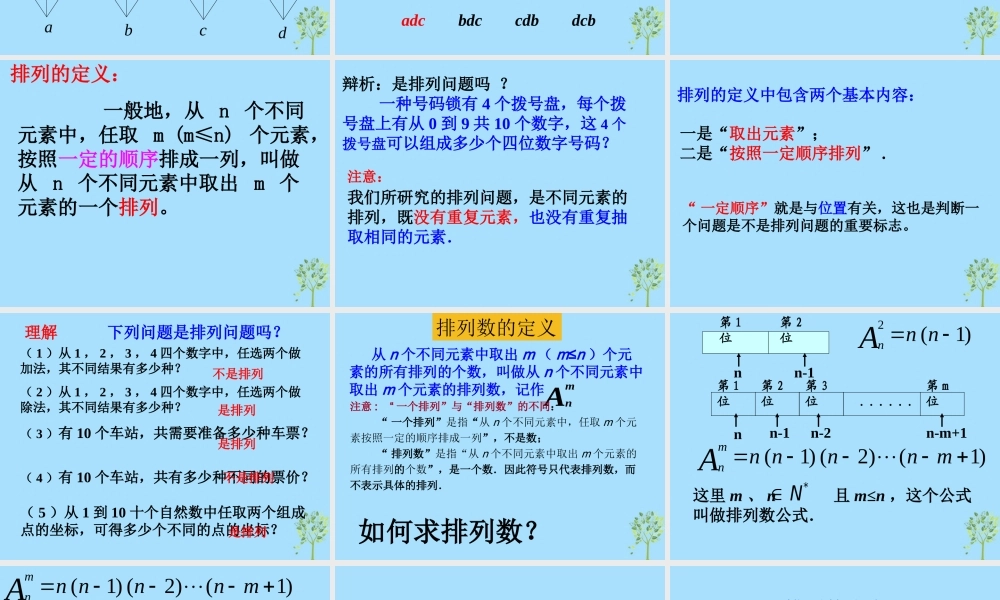
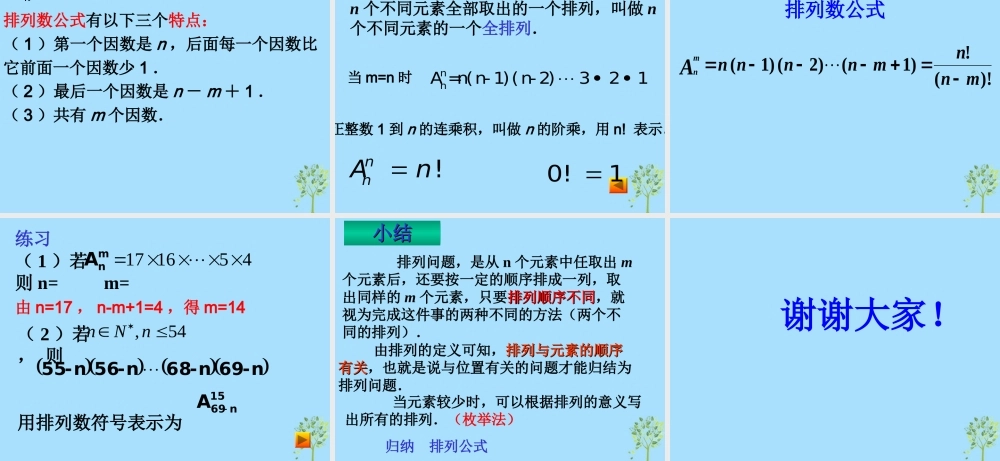
排 列排 列引例引例 问题问题 11 从甲、乙、丙 3 名同学中选出 2名参加某天的一项活动,其中 1 名同学参加上午的活动, 1 名同学参加下午的活动,有多少种不同的方法? 第 1 步,确定参加上午活动的同学,从 3 人中任选 1人有 3 种方法; 第 2 步,确定参加下午活动的同学,只能从余下的 2人中选,有 2 种方法. 根据分步计数原理分步计数原理,共有: 3×2 = 6 种不同的方法.解决这个问题,需分 22 个步骤个步骤:引例引例 问题问题 11 从甲、乙、丙 3 名同学中选出 2 名参加某天的一项活动,其中 1 名同学参加上午的活动, 1 名同学参加下午的活动,有多少种不同的方法?问题 1 就是:“从 3 名同学中任取 2名,然后按上下的顺序排成一列,求一共有多少种不同的排列方法 .”ac d b d b cb c dbcdb d a d a b b c a c a bc da ca da c da b da b c不同排法如下图所示 问题 2 从 a,b,c,d 这 4 个字母中 , 每次取出 3 个按顺序排成一列,共有多少种不同的排列方法?所有的排列为: abc bac cab dab abd bad cad dac acb bca cba dba acd bcd cbd dbc adb bda cda dca adc bdc cdb dcb 问题 2 就是“从 4 个不同的元素a 、 b 、c 、 d 中任取 3 个,然后按一定的顺序排成一列,求一共有多少种不同的排列 .”我们把问题 2 中被取的对象 ( 字母)叫做元素。 一般地,从 n 个不同元素中,任取 m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列。排列的定义:辩析:是排列问题吗 ? 一种号码锁有 4 个拨号盘,每个拨号盘上有从 0 到 9 共 10 个数字,这 4 个拨号盘可以组成多少个四位数字号码?我们所研究的排列问题,是不同元素的排列,既没有重复元素,也没有重复抽取相同的元素.注意:“ 一定顺序”就是与位置有关,这也是判断一个问题是不是排列问题的重要标志。一是“取出元素”;二是“按照一定顺序排列” .排列的定义中包含两个基本内容: 理解 下列问题是排列问题吗?( 1 )从 1 , 2 , 3 , 4 四个数字中,任选两个做加法,其不同结果有多少种?( 2 )从 1 , 2 , 3 , 4 四个数字中,任选两个做除法,其不同结果有多少种?( 3 )有 10 个车站,共需要准备多少种车票? ( 4 )有 10 个车站,共...