数学 2.1.2椭圆的简单几何性质(2)课件 新人教A版选修2 1 课件VIP免费

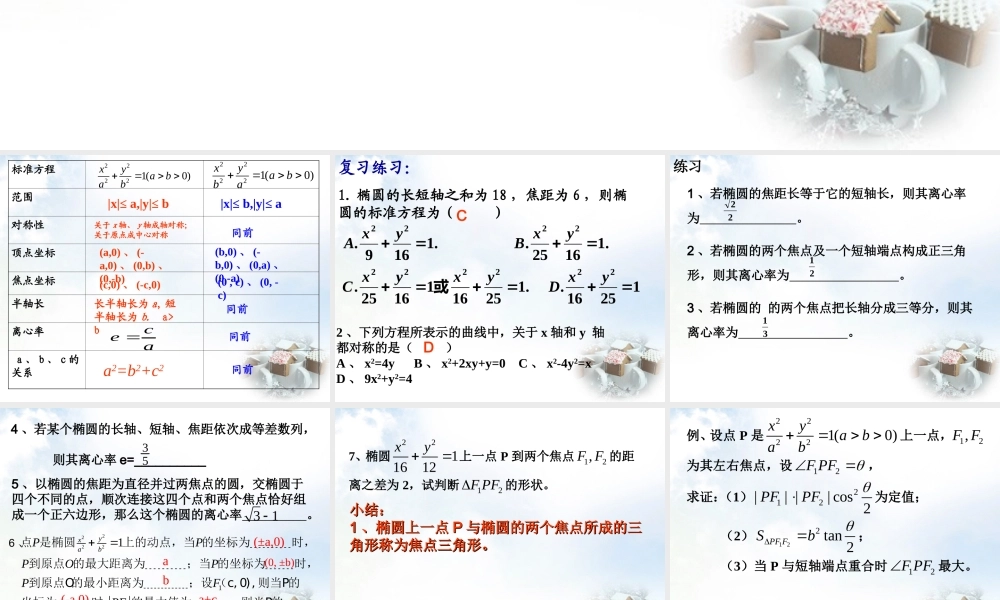
标准方程范围对称性顶点坐标焦点坐标半轴长离心率 a 、 b 、 c 的关系22221(0)xyabab|x|≤ a,|y|≤ b关于 x 轴、 y 轴成轴对称；关于原点成中心对称(a,0) 、 (-a,0) 、 (0,b) 、(0,-b)(c,0) 、 (-c,0)长半轴长为 a, 短半轴长为 b. a>bceaa2=b2+c222221(0)xyabba|x|≤ b,|y|≤ a同前(b,0) 、 (-b,0) 、 (0,a) 、(0,-a)(0 , c) 、 (0, -c)同前同前同前12516..1251611625..11625..1169.2222222222yxDyxyxCyxByxA或复习练习：1. 椭圆的长短轴之和为 18 ，焦距为 6 ，则椭圆的标准方程为（ ）2 、下列方程所表示的曲线中，关于 x 轴和 y 轴都对称的是（ ）A 、 x2=4y B 、 x2+2xy+y=0 C 、 x2-4y2=xD 、 9x2+y2=4CD练习1 、若椭圆的焦距长等于它的短轴长，则其离心率为 。2 、若椭圆的两个焦点及一个短轴端点构成正三角形，则其离心率为 。3 、若椭圆的 的两个焦点把长轴分成三等分，则其离心率为 。2221314 、若某个椭圆的长轴、短轴、焦距依次成等差数列， 则其离心率 e=__________5322221111yxabPPPOPPFPFPF                                        ---------------------------------点 是椭圆上的动点，当 的坐标为时，到原点 的最大距离为；当 的坐标为时，到原点O的最小距离为；设 （c, 0), 则当P的坐标为时，的最大值为；则当P的坐标为时，的最小值为。(±a,0)a(0, ±b)b(-a,0)a+c(a,0)a-c6 、5 、以椭圆的焦距为直径并过两焦点的圆，交椭圆于四个不同的点，顺次连接这四个点和两个焦点恰好组成一个正六边形，那么这个椭圆的离心率 。317、椭圆2211612xy 上一点 P 到两个焦点12,F F 的距离之差为 2，试判断12F PF的形状。 小结：小结：11 、椭圆上一点、椭圆上一点 PP 与椭圆的两个焦点所成的三与椭圆的两个焦点所成的三角形称为焦点三角形。角形称为焦点三角形。例、设点 P 是22221(0)xyabab上一点， 12,F F为其左右焦点，设12F PF， 求证：（1）212|| || cos 2PFPF为定值； （2）1 22 tan 2PF FSb； （3）当 P 与短轴端点重合时12F PF最大。 小结：已知椭圆方程为),0(12222babyax两焦点 分 别...