数学 第二章 变化率与导数及导数的应用 函数的极值课件 北师大版选修1-1 课件VIP免费

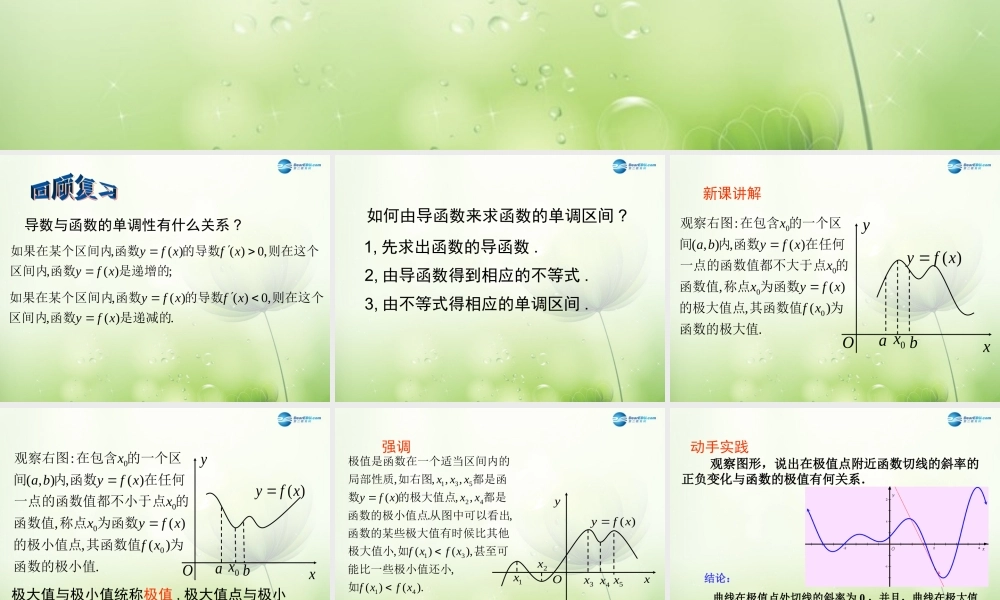
导数与函数的单调性有什么关系 ?;)(,,0)()(,是递增的函数区间内则在这个的导数函数如果在某个区间内xfyxfxfy.)(,,0)()(,是递减的函数区间内则在这个的导数函数如果在某个区间内xfyxfxfy如何由导函数来求函数的单调区间 ?1, 先求出函数的导函数 .2, 由导函数得到相应的不等式 .3, 由不等式得相应的单调区间 .新课讲解xyOab0x)(xfy .)(,)(,)(,),(:0000函数的极大值为其函数值的极大值点为函数称点函数值的点一点的函数值都不大于在任何函数内间的一个区在包含观察右图xfxfyxxxfybaxxyOab0x)(xfy .)(,)(,)(,),(:0000函数的极小值为其函数值的极小值点为函数称点函数值的点一点的函数值都不小于在任何函数内间的一个区在包含观察右图xfxfyxxxfybax极大值与极小值统称极值 , 极大值点与极小值点统称为极值点 .强调).()(,),()(,,.,,)(,,,,413142531xfxfxfxfxxxfyxxx如能比一些极小值还小甚至可如极大值小候比其他函数的某些极大值有时从图中可以看出函数的极小值点都是的极大值点数都是函如右图局部性质区间内的极值是函数在一个适当1x2xOy3x4x5xx)(xfy  观察图形，说出在极值点附近函数切线的斜率的正负变化与函数的极值有何关系． 曲线在极值点处切线的斜率为 0 ，并且，曲线在极大值点左侧切线的斜率为正，右侧为负；曲线在极小值点左侧切线的斜率为负，右侧为正．结论：动手实践 一般地，当函数 在点 处连续时，判断 是极大（小）值的方法是：0x)(xf)(0xf （ 1 ）如果在 附近的左侧 ，右侧 ，那么 是极大值．0x0)(0  xf0)(0  xf)(0xf （ 2 ）如果在 附近的左侧 ，右侧 ，那么 是极小值．0x0)(0  xf0)(0  xf)(0xf注：导数为 0 的点不一定是极值点．用图表示如下 :递增极大值 递减x),(0xa0x)(xf 0)(xfy ),( 0 bx递减极小值 递增x),(0xa0x)(xf 0)(xfy ),( 0 bxxya0xbOxya0xbO例题讲解.53632)(223的极值点求函数例xxxxf.320)()3)(2(63666)(::212xxxfxxxxxf和得到了两个解通过解方程数的导函数前面我们已求出这个函解.2,,)3,2(,0)(,32;)2,(,0)(,21是函数的极大值点因此上是递减的函数在时当上是递增的函数在时当xxfxxfx.3,;),3(,0)(,3,)3,2(,0)(,322是函数的极小值点因此上是递增的函数在时当上是递减的函数在时当xxfxxfx可用下...