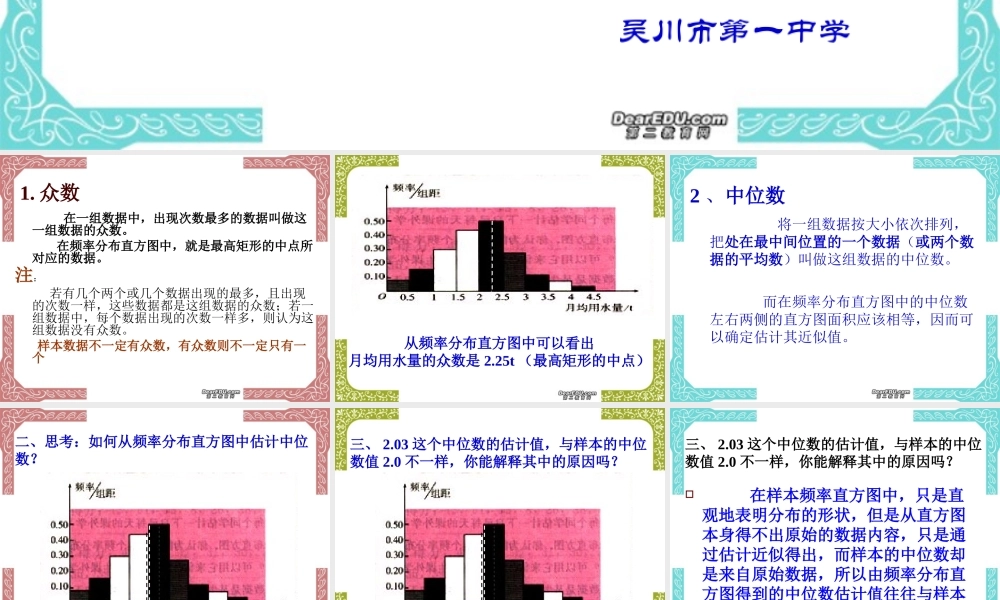
2.2.2 用样本的数字特征估计总体的数字特征吴川市第一中学1. 众数 在一组数据中,出现次数最多的数据叫做这一组数据的众数。 在频率分布直方图中,就是最高矩形的中点所对应的数据。注: 若有几个两个或几个数据出现的最多,且出现的次数一样,这些数据都是这组数据的众数;若一组数据中,每个数据出现的次数一样多,则认为这组数据没有众数。 样本数据不一定有众数,有众数则不一定只有一个从频率分布直方图中可以看出月均用水量的众数是 2.25t (最高矩形的中点)2 、中位数 将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数。 而在频率分布直方图中的中位数左右两侧的直方图面积应该相等,因而可以确定估计其近似值。二、思考:如何从频率分布直方图中估计中位数?三、 2.03 这个中位数的估计值,与样本的中位数值 2.0 不一样,你能解释其中的原因吗?三、 2.03 这个中位数的估计值,与样本的中位数值 2.0 不一样,你能解释其中的原因吗? 在样本频率直方图中,只是直观地表明分布的形状,但是从直方图本身得不出原始的数据内容,只是通过估计近似得出,而样本的中位数却是来自原始数据,所以由频率分布直方图得到的中位数估计值往往与样本的实际中位数不一致3. 平均数 设样本数据为 x1,x2,x3, …xn 那么样本平均数为 X=1/n(x1+x2+……+xn) 平均数描述了数据的平均水平 , 定量地反映了数据的集中趋势所处的水平用样本平均数估计总体平均数 从一个总体中随机抽取的一个容量一定的包含了大量数据的样本 , 利用样本平均数的计算公式求出样本平均数 , 由此得出样本平均数近似等于总体平均数 .思考 ?? 为什么不是等于 , 而是近似等于 ? 两次从总体中抽取容量相等的样本 ,分别求出样本平均数 , 两个样本平均数会不相同 , 所以用样本平均数估计总体平均数时 , 样本平均数只是总体平均数的近似值四、阅读课本 63 页的思考,举例分析对极端值不敏感的利与弊。五、练习 应该采用平均数来表示每一个国家项目的平均金额,因为它能反映所有项目的信息。但平均数会受到极端数据 2200 万元的影响,所以大多数项目投资金额都和平均数相差比较大。