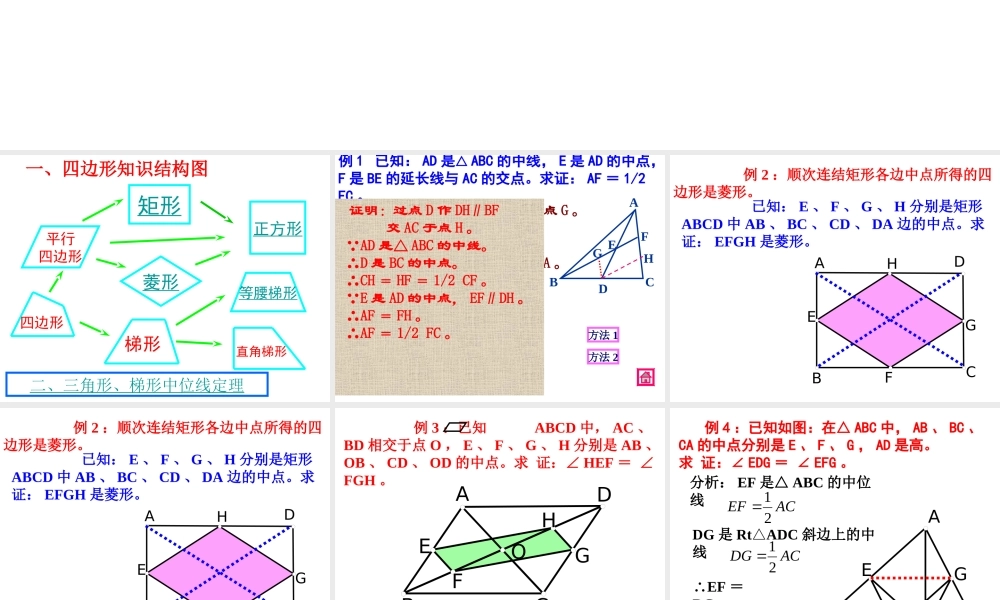
证明复习一、四边形知识结构图四边形平行四边形矩形菱形正方形梯形等腰梯形直角梯形二、三角形、梯形中位线定理例 1 已知: AD 是△ ABC 的中线, E 是 AD 的中点,F 是 BE 的延长线与 AC 的交点。求证: AF = 1/2 FC 。ABCDEFG证明 : 过点 D 作 DG∥AC 交 BF 于点 G 。∴∠ GDE =∠ FAE 。 E 是 AD 的中点。∴DE = AE 。又 ∠ GED =∠ FEA 。∴△DEG≌△AEF ∴DG = AF 。 DG∥AC , BD = DC 。∴BG = GF 。∴DG 是△ BCF 的中线。∴DG = 1/2 FC 。∴AF = 1/2 FC 。H 证明:过点 D 作 DH∥BF 交 AC 于点 H 。 AD 是△ ABC 的中线。 ∴D 是 BC 的中点。 ∴CH = HF = 1/2 CF 。 E 是 AD 的中点, EF∥DH 。 ∴AF = FH 。 ∴AF = 1/2 FC 。方法 1方法 2HGFEDCBA 例 2 :顺次连结矩形各边中点所得的四边形是菱形。 已知: E 、 F 、 G 、 H 分别是矩形ABCD 中 AB 、 BC 、 CD 、 DA 边的中点。求证: EFGH 是菱形。HGFEDCBA 例 2 :顺次连结矩形各边中点所得的四边形是菱形。 已知: E 、 F 、 G 、 H 分别是矩形ABCD 中 AB 、 BC 、 CD 、 DA 边的中点。求证: EFGH 是菱形。GHFOEDCBA 例 3 :已知 ABCD 中, AC 、BD 相交于点 O , E 、 F 、 G 、 H 分别是 AB 、OB 、 CD 、 OD 的中点。求 证:∠ HEF = ∠FGH 。 例 4 :已知如图:在△ ABC 中, AB 、 BC 、CA 的中点分别是 E 、 F 、 G , AD 是高。求 证:∠ EDG = ∠ EFG 。GFEDCBA分析: EF 是△ ABC 的中位线ACEF21DG 是 RtADC△斜边上的中线ACDG21∴EF =DG你还想到了什么? 例 5 :已知 : 如图 , 梯形 ABCD 中, AB∥CD,以 AD 和 AC 为边作平行四边形 ACED,DC 的延长线交 BE 于点 F, 求证 :EF = FBFEDCBAO利用平行四边形 ACED 的性质可知 AO=EO ,即可证得结论。一、判断题:1 )两条对角线相等且互相垂直的四边形是矩形 . ( )2 )两条对角线互相垂直平分的四边形是菱形 . ( )3 )两条对角线互相垂直的矩形是正方形 . ( )4 )两条对角线相等的菱形是正方形 . ( )5 )两条对角线垂直且相等的平行四边形是正方形 .( )6 )两条对角线垂直且相等的四边形是正方形 . ( )课堂练习...