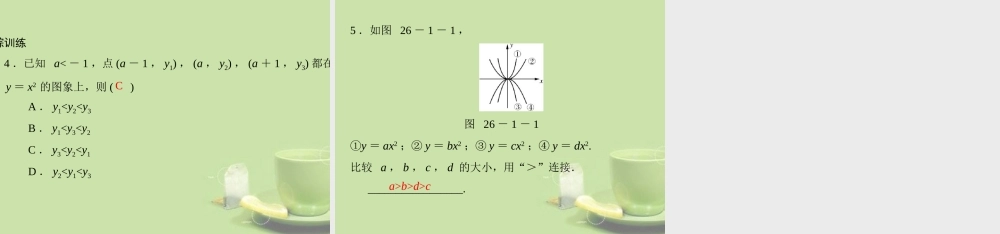
下册 第二十六章 二次函数 26.1第 1 课时二次函数及其图象二次函数及 y = ax 的图象21 .二次函数的概念(1) 形如 y = ax2 + bx + c(a , b , c 是 ______ , a____) 的函数,叫做二次函数.常数≠0xabc(2)______ 是自变量, ______ , ______ , ______ 分别是函数表达式的二次项系数、一次项系数和常数项.2 .描点法作图的三个步骤列表描点连线(1)________ ; (2)________ ; (3)________ .3 .顶点对称轴低高(1) 定义:抛物线与 ________ 的交点.(2) 性质:抛物线的最 ______ 点或最 ______ 点.4 .二次函数 y = ax2 的图象探究: y = ax2 ,≥上≤下(1) 当 a>0 时,无论 x 取何值,总有 y____0 ,除点 (0,0) 外,抛物线在 x 轴 ____ 方.(2) 当 a<0 时,无论 x 取何值,总有 y____0 ,除点 (0,0) 外,抛物线在 x 轴 ____ 方.函数 a 的符号图象开口方向对称轴顶点坐标有最高或最低点最值y = ax2a>0向上y 轴(0,0)最低点当 x =0 时,ymin = 0a<0向下最高点当 x =0 时,ymax = 0归纳:当 a<0 时, a 越大,抛物线的开口越 ______ .小大(3) 当 a>0 时, a 越大,抛物线的开口越 ______ ;二次函数的概念 ( 重点 )例 1:当 m 为何值时,y=(m2-4)24mmx +2x-1 是关于 x的二次函数? 思路点拨:根据二次函数的定义,要使 y=(m2-4)24mmx +2x-1 是二次函数,m 必须满足两个条件:①m2-m-4=2; ②m2-4≠0.两者缺一不可. 自主解答:根据题意,得 m2-m-4=2,m2-4≠0. 解得 m=3. ∴当 m=3 时,y=(m2-4)24mmx +2x-1 是二次函数. 跟踪训练1 .下列函数中是二次函数的是 ()AA.y=2x2 B.y= x2-1 C.y=1x2 D.y=a2x 2.已知 y=(m-3)2 7mx 是 y 关于 x 的二次函数,求 m 的值. 解:由题意,得 m2-7=2,m-3≠0,解得 m=-3. 二次函数 y = ax2 的图象的画法例 2:在同一直角坐标中,画出函数 y=12x2 和 y=-2x2 的图象,并根据图象回答下列问题: (1)说出这两个函数图象的开口方向、对称轴和顶点坐标; (2)抛物线 y=12x2,当 x________时,抛物线上的点都在 x 轴上方;当 x>0 时,曲线自左向右逐渐________;它的顶点是图象的最________点; (3)函数 y=-2x2,对于一切 x 的值,总有函数值...