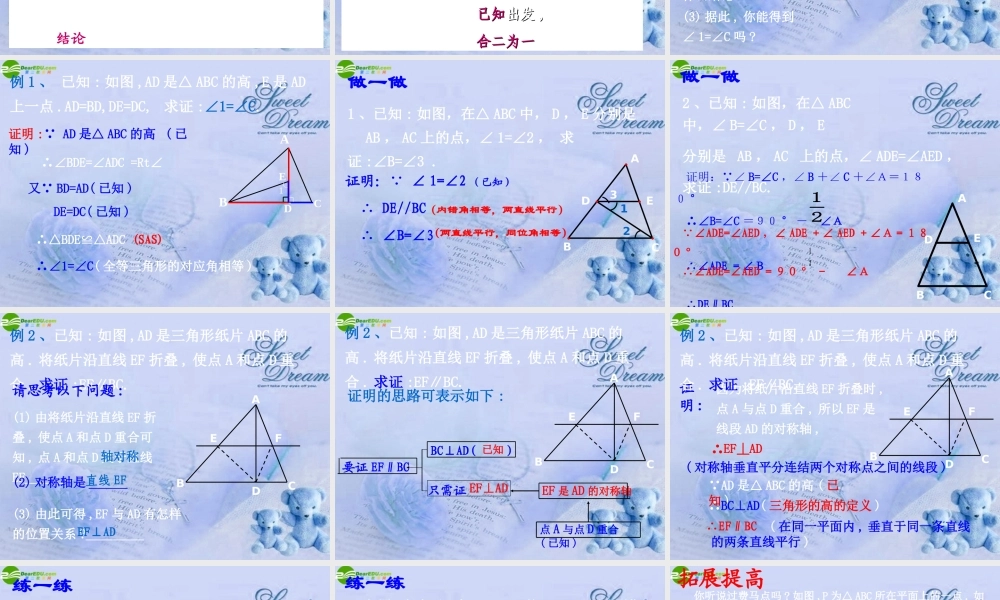
证明题表述的一般格式:1 、按题意画出图形;2 、分清命题的条件和结论,结合图形,在”已知“中定出条件,在”求证“中写出结论。3 、在”证明“中写出推理过程。温故知新你会判定两个三角形全等吗 ? 有哪些方法 ?(1)SSS(2)SAS(3)ASA(AAS)(4)HL( 用于两个直角三角形全等的判定 )温故知新1 、已知 : 如图 ,AD∥BC, ∠B=∠D.求证 :△ADC≌△CBA.ABCD分析 : 要证△ ADC≌△CBA.∠B=∠D( 已知 )AC=CA( 公共边 )只需证∠ BAC=∠DCA 或∠ ACB=∠CADAD∥BC( 已知 )小试身手 从要证明的结论结论出发 , 探索要使结论成立 ,需要什么条件需要什么条件 , 并与已知对照 , 充分利用已知条件 , 直至找到需要 , 并且这个最后的需要是已知的已知的条件条件 , 从而达到证明的目的 .2 、已知 : 如图 , 在四边形 ABCD中 ,AD∥BC,AB∥CD.求证 :△ABD≌△CDB.ABCD分析 :△ABD≌△CDBAD∥BC,AB∥CD( 已知 )∠BDC=∠DBA∠CBD=∠ADB小试身手 要证明一个结论 , 也可以从已知已知出发 , 推出可能的结果 , 并与证明的结论比较 , 直至推出要证明的结论 .3 、已知 : 如图 , 在四边形 ABCD中 ,AD=BC,AB=CD.求证 : AD∥BC,AB∥CD.ABCD分析 :AD=BC,AB=CD( 已知 )要证 AD∥BC,AB∥CD需证∠ BDC=∠DBA 及∠ CBD=∠ADB△ABD≌△CDB小试身手 要证明一个结论 , 可以从结论出发 , 探求需要什么条件 ; 再从已知已知出发出发 ,, 推出可能的结果 ; 两者比较 , 直至合二为一合二为一 .例 1 、 已知 : 如图 ,AD 是△ ABC 的高 ,E 是 AD上一点 .AD=BD,DE=DC, 求证 :∠1=∠C.⌒BCDE1∟A想一想 :(1) 由已知 AD 是△ ABC 的高 , 可以得到什么 ?(2) 由已知 AD=BD,DE=DC, ∠BDE=Rt∠=∠ADC, 可以得到什么结论 ?(3) 据此 , 你能得到∠ 1=∠C 吗 ?⌒BCDE1∟A证明 : AD 是△ ABC 的高 ( 已知 )∴∠BDE=∠ADC =Rt∠又 BD=AD( 已知 ) DE=DC( 已知 )∴△BDE≌△ADC∴∠1=∠C( 全等三角形的对应角相等 )(SAS)例 1 、 已知 : 如图 ,AD 是△ ABC 的高 ,E 是 AD上一点 .AD=BD,DE=DC, 求证 :∠1=∠C.1 、已知 : 如图,在△ ABC 中, D , E 分别是 AB , AC 上的点,∠ 1=∠2 , 求证 :∠B=∠3 .C123ABDE证明: ∠ 1=∠2 (已知) ∴ DE//BC ∴ ∠B=∠3(内错角相等,两直线平行) (两直线平行,同位角相等...