九年级数学二次根式除法课件 华师大版 课件VIP免费

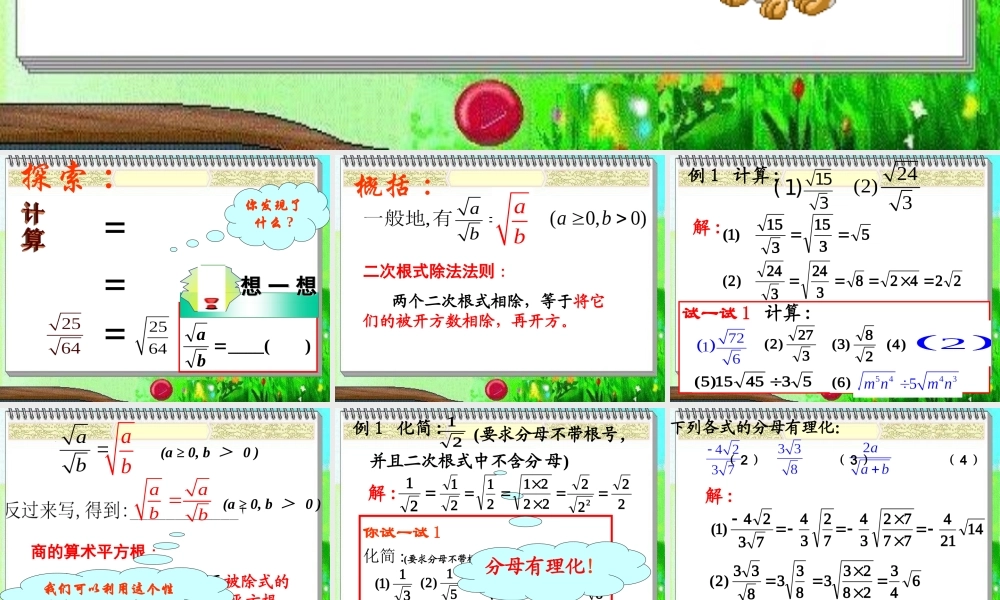
§22.2.3 探索 :你发现了什么 ?)____(ba想想 一一 想想想想 一一 想想 ab二次根式除法法则 : 两个二次根式相除，等于将它们的被开方数相除，再开方。概括 : 24(2)3例 1 计算 :)()(试一试 1 计算 :)()()()()(解 : 商的算术平方根 : 商的算术平方根，等于被除式的算术平方根除以除式的算术平方根。aabbab(a ≥ 0, b ＞ 0 )我们可以利用这个性质进行二次根式的化简！(a ≥ 0, b ＞ 0 ) 例 1 化简 :),(母并且二次根式中不含分要求分母不带根号解 : 你试一试 1化简 :)()()()()(),(母并且二次根式中不含分要求分母不带根号分母有理化！ 例 2 把下列各式的分母有理化：（ 1 ） （ 2 ） （ 3 ） （ 4 ）解 : )()(分母有理化，应找最简单的有理化因式 例 2 把下列各式的分母有理化：（ 1 ） （ 2 ） （ 3 ） （ 4 ）解 : baa)(xx)(bababaababaaxxxxxxxx 例 3 分母有理化：263xx解：方法 2232223223263xx)x(x)(xxx比较两种方法的依据各是什么？哪种方法更简便？23222322263263xxx)(x)x(x)x(xx方法 1分母有理化，也可灵活运用我们学过的性质和法则，简化、优化解答过程。 试一试 2 把下列各式分母有理化：        xxmmmyxyxaa最简二次根式！（ P9 ） 判断下列各等式是否成立。（ 1 ） （ ）（ 2 ） （ ） （ 3 ） （ ）（ 4 ） （ ）349162323 212214592952×××√辨析训练辨析训练 观察、猜想训练观察、猜想训练    验证下列各式，猜想下一个式子是什么？你能找到反映上述各式的规律吗？nnnnnnn 小结小结二次根式...