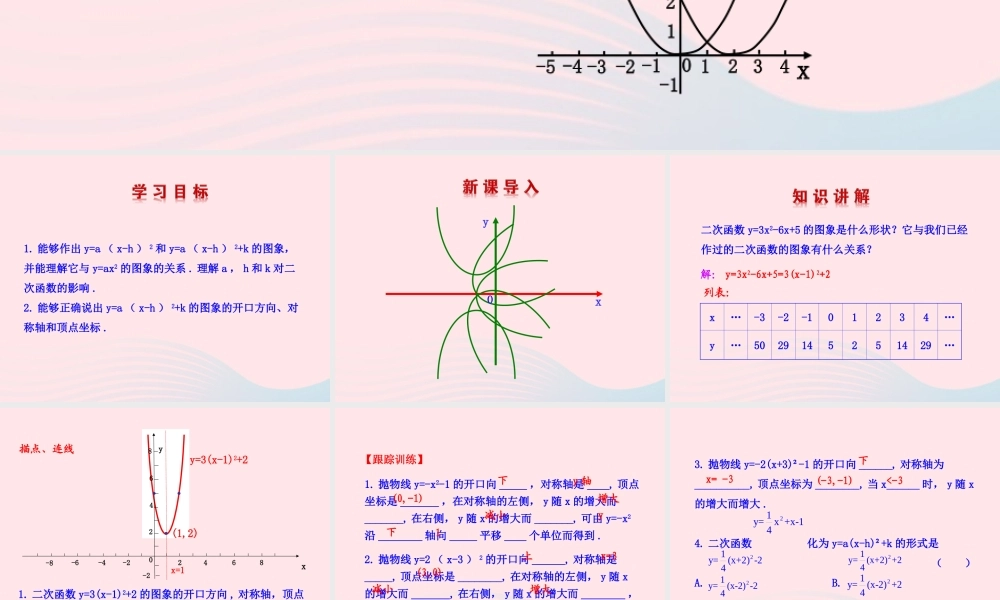
2. 二次函数 y=ax2+bx+c 的图象与性质 ( 第 3 课时 )y21y=x221y=(x-22)-1-2-3-5 -412 34-112340x1. 能够作出 y=a ( x-h ) 2 和 y=a ( x-h ) 2+k 的图象,并能理解它与 y=ax2 的图象的关系 . 理解 a , h 和 k 对二次函数的影响 .2. 能够正确说出 y=a ( x-h ) 2+k 的图象的开口方向、对称轴和顶点坐标 .xyO二次函数 y=3x2-6x+5 的图象是什么形状?它与我们已经作过的二次函数的图象有什么关系?解: y=3x2-6x+5=3(x-1)2+2列表:x…-3-2-101234…y…5029145251429… xy=3(x-1)2+2x=1y描点、连线-2-4-68642 0-8 -2(1,2) 2 4 6 81. 二次函数 y=3(x-1)2+2 的图象的开口方向 , 对称轴,顶点坐标和增减性分别是什么 ?2. 它与抛物线 y=3x² 有什么关系 ?1. 抛物线 y=-x2-1 的开口向 _____ ,对称轴是 ____, 顶点坐标是 _______ ,在对称轴的左侧, y 随 x 的增大而_______, 在右侧, y 随 x 的增大而 _______, 可由 y=-x2沿 ________ 轴向 _____ 平移 ____ 个单位而得到 .2. 抛物线 y=2 ( x-3 ) 2 的开口向 ______, 对称轴是_____, 顶点坐标是 ________, 在对称轴的左侧, y 随 x的增大而 _______, 在右侧, y 随 x 的增大而 ________ ,可由 y=2x2 沿 _____ 轴向 ______ 平移 ______ 个单位而得到 .下y 轴(0,-1)增大减小y下1上x=3(3,0)减小增大3x右【跟踪训练】3. 抛物线 y=-2(x+3)²-1 的开口向 ______, 对称轴为__________, 顶点坐标为 ________, 当 x______ 时, y 随 x的增大而增大 . 4. 二次函数 化为 y=a(x-h)²+k 的形式是( )A. B.C. D.下x= -3(-3,-1)<-3【答案】 A21y=x +x-1421y=(x+2) -2421y=(x+2) +2421y=(x-2) -2421y=(x-2) +245. 抛物线 y=3x² 先向上平移 2 个单位,后向右平移 3 个单位,所得到的抛物线是( ) A.y=3(x+3)²-2 B.y=3(x+3)²+2 C.y=3(x-3)²-2 D.y=3(x-3)²+26. 某二次函数的图象向左平移 2 个单位,然后向上平移 3个单位后,得到的函数表达式是 y=2x² ,则原函数关系式是_______________.【答案】 Dy=2(x-2)2-37. 如图,抛物线的顶点 P 的坐标是( 1 , -3 ),则此抛物线对应的二次函数有( ) A. 最大值 1 B. 最小值 -3 C. 最大值 -3 D. 最小值 1OxyP【答案】 B8. 已知二次函数 y=a(x+1)²+c 的图...