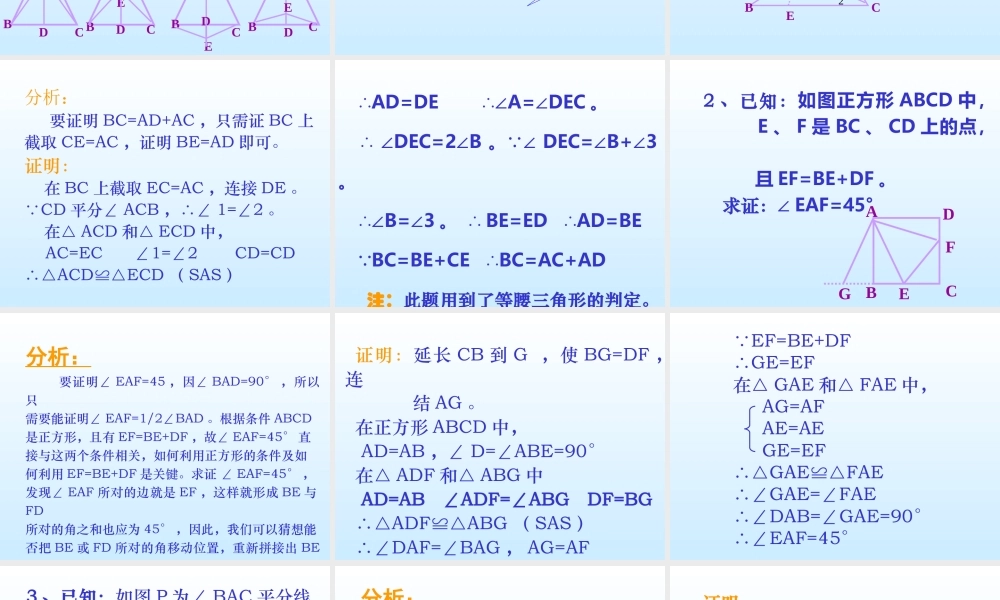
基础教育同步课堂九年级 数 学全等三角形综合课 教学目的: 1 、使学生对三角形的判定与性质有进 一步综合运用的能力,对复杂的几 何证明题能够综合分析,找到解决 问题的途径。 2 、培养学生综合分析问题,解决问题 的能力,对图形变化感知的能力。 教学重点、难点: 图形变化的认知,以及添加辅助线的方法。重点、难点重点、难点 复习:复习: 1 、全等三角形的判定方法: 定义、 SAS 、 ASA 、 AAS 、 SSS 。 2 、复习证明。 ( 1 )已知:如图:△ ABC 中, AB=AC , D 为 BC 的中点, E 为 AD 上任意一点。 求证: BE=EC (观察:随着 E 点的变化, BE , EC 的关系不变)。EAAAABBBBCCDCDDDCEEE 思考:思考: 1 )此时 AD 为△ ABC 的什么线? 2 ) E 为 AD 上一动点,是否总保 持 BE=EC 。思考思考 新课新课 1 、已知:如图∠ A=2∠B , CD 平分 ∠ACB , 求证: BC=AD+AC (翻拆变换)ABCDE123 分析: 要证明 BC=AD+AC ,只需证 BC 上截取 CE=AC ,证明 BE=AD 即可。证明: 在 BC 上截取 EC=AC ,连接 DE 。 CD 平分∠ ACB ,∴∠ 1=∠2 。 在△ ACD 和△ ECD 中, AC=EC ∠1=∠2 CD=CD∴△ACD≌△ECD ( SAS ) ∴AD=DE ∴∠A=∠DEC 。 ∴ ∠DEC=2∠B 。 ∠ DEC=∠B+∠3。 ∴∠B=∠3 。 ∴ BE=ED ∴AD=BE BC=BE+CE ∴BC=AC+AD 注:此题用到了等腰三角形的判定。 2 、已知:如图正方形 ABCD 中, E 、 F 是 BC 、 CD 上的点, 且 EF=BE+DF 。 求证:∠ EAF=45° ABCDEFG 分析: 要证明∠ EAF=45 ,因∠ BAD=90° ,所以只需要能证明∠ EAF=1/2∠BAD 。根据条件 ABCD是正方形,且有 EF=BE+DF ,故∠ EAF=45° 直接与这两个条件相关,如何利用正方形的条件及如何利用 EF=BE+DF 是关键。求证 ∠ EAF=45° ,发现∠ EAF 所对的边就是 EF ,这样就形成 BE 与FD所对的角之和也应为 45° ,因此,我们可以猜想能否把 BE 或 FD 所对的角移动位置,重新拼接出 BE+DF 所对的角,只需证明这个角为 45° 即可。 证明:延长 CB 到 G ,使 BG=DF ,连 结 AG 。在正方形 ABCD 中, AD=AB ,∠ D=∠ABE=90°在△ ADF 和△ ABG 中 AD=AB ∠ADF=∠ABG DF=BG∴△ADF≌△ABG ( SAS )∴∠DAF=∠BAG , AG=AF EF=BE+DF∴GE=EF在△ ...