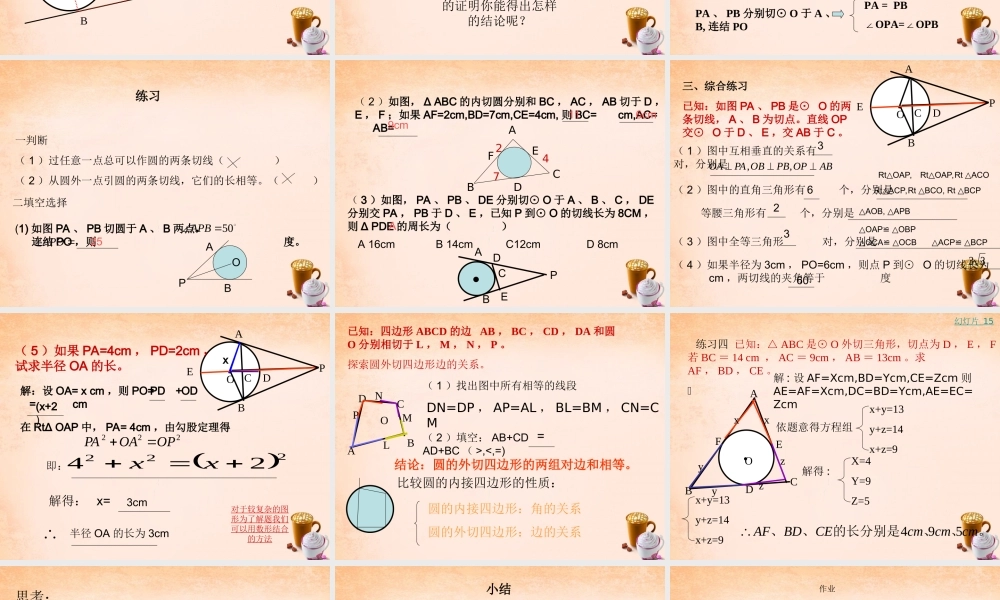
(1) 和圆有唯一公共点的直线叫 ( 2 )圆的切线 过切点的半径。 ( 3 )四边形 ABCD 各边都和⊙ O 相切,则四边形ABCD 叫做这个圆的圆的切线垂直于外切四边形一复习APB 这是一位同学运动完后放的篮球,如果截它的平面,那么你能从中发现什么几何知识呢?墙 地面 P经过圆外一点可以有两条直线与圆相切二探索PBCO切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长。思考:切线长和切线的区别和联系?小结:切线是直线,不可以度量;切线长是小结:切线是直线,不可以度量;切线长是指切线上的一条线段的长,可以度量。指切线上的一条线段的长,可以度量。下面进一步探讨,先请一些同学做小实验:pABO12( 1 )请同学们观察当圆变化时,切线长 PA 、 PB之间的关系,同时注意 之间的关系。21 、( 2 )请根据你的观察尝试总结它们之间的关系。pABO已知: 求证:如图, P 为⊙ O 外一点, PA 、 PB 为⊙ O的切线, A 、 B 为切点,连结 POBPOAPOPBPA,你能不能用所学的几何知识证明刚才的实验?从你实验的观察和你的证明你能得出怎样的结论呢?切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。pABO请你们结合图形用数学语言表达定理PA 、 PB 分别切⊙ O 于 A 、B, 连结 POPA = PB∠OPA=OPB∠一判断( 1 )过任意一点总可以作圆的两条切线( )( 2 )从圆外一点引圆的两条切线,它们的长相等。( )练习(1) 如图 PA 、 PB 切圆于 A 、 B 两点, 连结 PO ,则 度。50APBAPO25PBOA二填空选择( 2 )如图, Δ ABC 的内切圆分别和 BC , AC , AB 切于 D ,E , F ;如果 AF=2cm,BD=7cm,CE=4cm, 则 BC= cm,AC= AB= ( 3 )如图, PA 、 PB 、 DE 分别切⊙ O 于 A 、 B 、 C , DE分别交 PA , PB 于 D 、 E ,已知 P 到⊙ O 的切线长为 8CM ,则 Δ PDE 的周长为( )A 16cmD 8cmC12cmB 14cm APDCBE116cm9cmABDACFE274三、综合练习已知:如图 PA 、 PB 是⊙ O 的两条切线, A 、 B 为切点。直线 OP交⊙ O 于 D 、 E ,交 AB 于 C 。OPABCDE( 1 )图中互相垂直的关系有 对,分别是( 2 )图中的直角三角形有 个,分别是等腰三角形有 个,分别是( 3 )图中全等三角形 对,分别是( 4 )如果半...