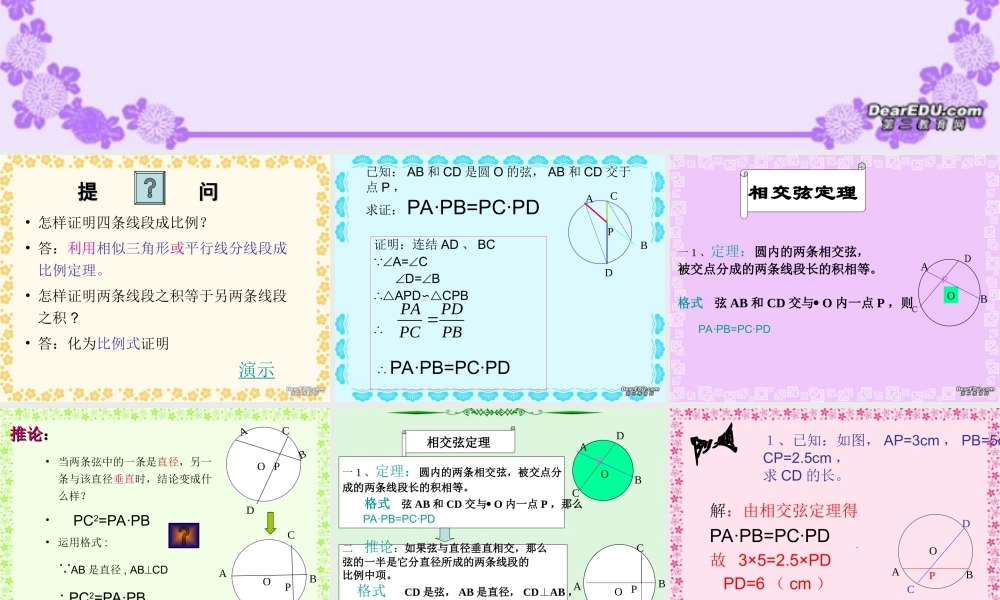
相交弦定理相交弦定理相交弦定理相交弦定理提 问提 问• 怎样证明四条线段成比例?• 答:利用相似三角形或平行线分线段成比例定理。• 怎样证明两条线段之积等于另两条线段之积 ?• 答:化为比例式证明演示已知: AB 和 CD 是圆 O 的弦, AB 和 CD 交于点 P ,求证: PA·PB=PC·PD证明:连结 AD 、 BC A=C D=B∴APD∽CPB∴ ∴ PA·PB=PC·PDABPCDPAPDPCPB一 1 、定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。 格式 弦 AB 和 CD 交与 O 内一点 P ,则 PA·PB=PC·PDOABP相交弦定理DC推论推论::• 当两条弦中的一条是直径,另一条与该直径垂直时,结论变成什么样?• PC2=PA·PB• 运用格式 : AB 是直径 , ABCD PC2=PA·PBPABCDOABCDPO演示O一 1 、定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。 格式 弦 AB 和 CD 交与 O 内一点 P ,那么 PA·PB=PC·PDOABCDP相交弦定理二 推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。 格式 CD 是弦, AB 是直径, CDAB⊥,垂足是 P , 则 PC2=PA·PB CDABP1、已知:如图, AP=3cm , PB=5cm ,CP=2.5cm ,求 CD 的长。解:由相交弦定理得PA·PB=PC·PD故 3×5=2.5×PD PD=6 ( cm ) CD=6+2.5=8.5(cm)答 :CD=8.5cm 。OCDABP·2 、已知圆中的两条弦相交,第一条被交点分为12cm 和 16cm 两段,第二条弦的长为 32cm ,求第二条弦被交点分成的两段的长。解:设第二条弦被交点分成的一段长为 xcm ,则另一段长为( 32-x ) cm 。 由相交弦定理得 1216x(32-X)22 x 32-x =12 16 32x-x =192 x -32x+192=0 ( x-8) (x-24)=0 x=8x=24故或故另一段长为 32 - 8=24 或 32 - 24=8答:另一弦被交点分成的两段长分别为 8cm 、 24cm解 过 OP 作直径 CD ,设圆 O 的半径为 xcm ,由相交弦定理得,PD*PC=PA*PB( x-5 ) * ( x+5 ) =6*4x2-25=24 x2=49 x=7 或 x=-7 (舍去)答:圆 O 的半径为 7cm 。已知:如图, AB 是圆 O 的弦, P 是 AB上的一点, AB=10cm , OP=5cm ,PA=4cm ,求圆 O 的半径。O例题例题PABCD DC已知:如图 AB 是 O 的直径, ABCD ,垂足为 P , CP=4cm , PB=2cm ,求 PO的长。解 :AB 是直径, ABCD P...