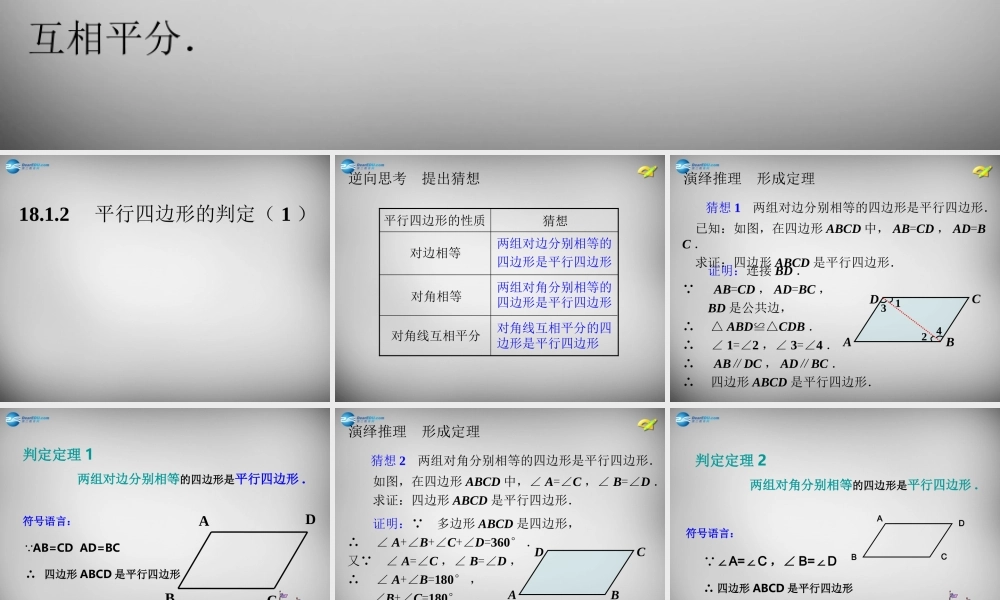
平行四边形的定义:两组对边分别平行的四边形叫做平行四边形. 平行四边形的性质:对边相等,对角相等,对角线互相平分.判定性质定义复习反思 引出课题 D A B C 18.1.2 平行四边形的判定( 1 )逆向思考 提出猜想 两组对边分别相等的四边形是平行四边形 平行四边形的性质 猜想 对边相等 对角相等 对角线互相平分 两组对角分别相等的四边形是平行四边形 对角线互相平分的四边形是平行四边形 证明:连接 BD . AB=CD , AD=BC , BD 是公共边,∴ △ ABD≌△CDB .∴ ∠ 1=∠2 ,∠ 3=∠4 .∴ AB∥DC , AD∥BC .∴ 四边形 ABCD 是平行四边形. 已知:如图,在四边形 ABCD 中, AB=CD , AD=BC . 求证:四边形 ABCD 是平行四边形. 演绎推理 形成定理 两组对边分别相等的四边形是平行四边形. 猜想 1 D A B C 1234驶向胜利的彼岸判定定理 1 两组对边分别相等的四边形是平行四边形 .BCAD符号语言: AB=CD AD=BC∴ 四边形 ABCD 是平行四边形 证明: 多边形 ABCD 是四边形,∴ ∠ A+∠B+∠C+∠D=360° .又 ∠ A=∠C ,∠ B=∠D ,∴ ∠ A+∠B=180° , ∠B+∠C=180° . ∴ AD∥BC , AB∥DC .∴ 四边形 ABCD 是平行四边形. 如图,在四边形 ABCD 中,∠ A=∠C ,∠ B=∠D . 求证:四边形 ABCD 是平行四边形. 演绎推理 形成定理 两组对角分别相等的四边形是平行四边形. 猜想 2 D A B C 判定定理 2 两组对角分别相等的四边形是平行四边形 .驶向胜利的彼岸符号语言: ∠A=C∠,∠ B=D∠∴ 四边形 ABCD 是平行四边形ABCD如图,在四边形 ABCD 中, AC , BD 相交于点 O ,且OA=OC , OB=OD .求证:四边形 ABCD 是平行四边形. 演绎推理 形成定理 对角线互相平分的四边形是平行四边形. D A B C O 猜想 3 证明: OA=OC , OB=OD ,∠ AOD=∠COB , ∴ △ AOD≌△COB .∴ ∠ OAD=∠OCB .∴ AD∥BC .同理 AB∥DC .∴ 四边形 ABCD 是平行四边形.判定定理 3 对角线互相平分的四边形是平行四边形 .驶向胜利的彼岸ABCDO符号语言: OA=OC , OB=OD∴ 四边形 ABCD 是平行四边形 现在,我们一共有哪些判定平行四边形的方法呢? 定义:两组对边分别平行的四边形叫做平行四边形. 判定定理: ( 1 )两组对边分别相等的四边形是平行四边形;( 2...