八年级数学上册 15.1.3积的乘方课件 人教新课标版 课件VIP免费

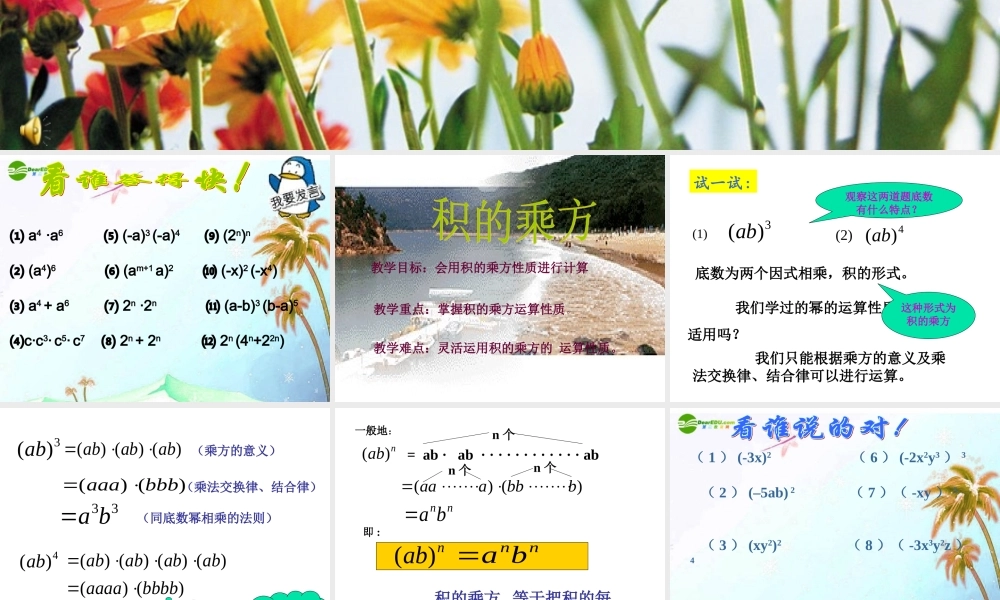
⑴ a4 ·a6 (-a)⑸3 (-a)4 (2⑼n)n ⑵ (a4)6 (a⑹m+1 a)2 (-x)⑽2 (-x4) ⑶ a4 + a6 2⑺n ·2n (a-b)⑾3 (b-a)5⑷c·c3· c5· c7 2⑻n + 2n 2⑿n (4n+22n) 教学目标：会用积的乘方性质进行计算 教学重点：掌握积的乘方运算性质。教学难点：灵活运用积的乘方的 运算性质。试一试 :3)(ab4)(ab(1)(2) 我们只能根据乘方的意义及乘法交换律、结合律可以进行运算。观察这两道题底数有什么特点？底数为两个因式相乘，积的形式。 我们学过的幂的运算性质适用吗？这种形式为积的乘方 3)(ab)()()(ababab)()(bbbaaa 33ba4)(ab)()()()()()(bbbbaaaaabababab44ba（乘方的意义）（乘法交换律、结合律）（同底数幂相乘的法则）积的乘方有什么规律呢？一般地：nab)()()(bbbaaannban 个n 个n 个即 : 积的乘方 , 等于把积的每一因式分别乘方 , 再把所得的幂相乘 .= ab · ab · · · · · · · · · · · · abnab)(nnba （ 1 ） (-3x)2 （ 6 ） (-2x2y3 ） 3 （ 2 ） (–5ab) 2 （ 7 ）（ -xy ） 5 （ 3 ） (xy2)2 （ 8 ）（ -3x3y2z ）4 （ 4 ）（ 5ab2 ） 3 （ 9 ）（ 2×102 ） 3（ 5 ） (-2xy3z2)4 （ 10 ）（ -3×103 ） 2 ⑴⑵⑶⑷224)412(12124250125025052 3332221 小组合作题（ 1 ）若 x-y = a ，则（ 3x-3y ） 3 = ，（ 2 ）若 813×274 = x24 ，则 x = ， 若 813×274 = y12 ，则 y = 。（ 3 ）比较 813 与 274 大小27a339 讨 论 题： nmnnmaaaa42262，求，已知：nnabba)1( 02351223 bAaabbamnm求 m 、 n 、 A 的值 课堂小结：（ 1 ）本节课学习了积的乘方的运算性质 积的乘方等于把积的每一个因式乘方后，再把所得的幂相乘。（ 2 ）学习了一种常见的数学方法： 把某个式子看作一个数或字母。 （ 3 ）今后学习中要注意灵活运用积的乘方的 运算性质，注意符号的确定和逆向运用。