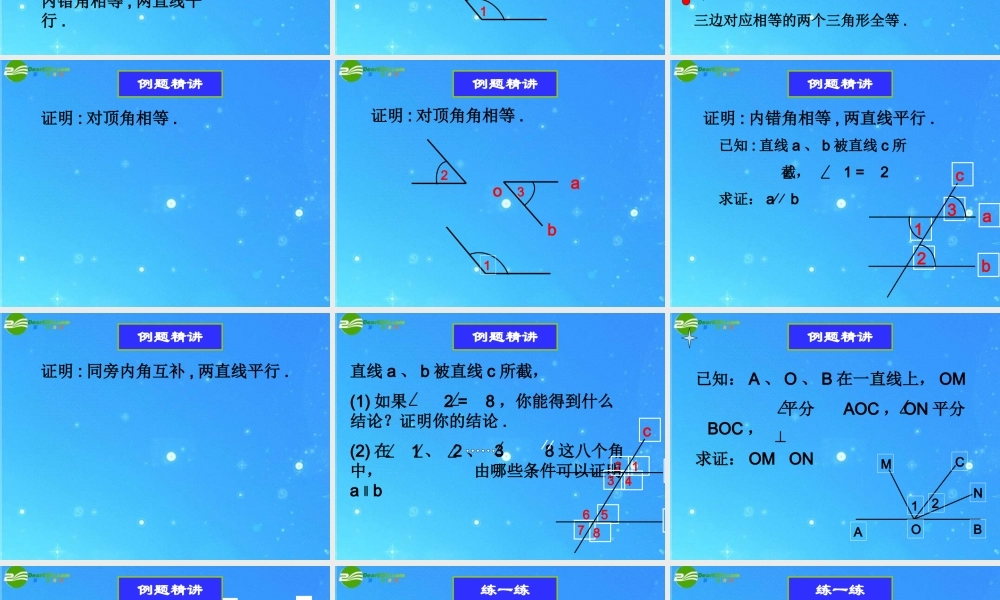
初中数学八年级下册(苏科版)11.3 证明( 1 )• 一个数学的结论的正确性是如何确认的?• 其实数学家们早就遇到了这样的问题,人类对数学命题进行证明的研究已有 2000 年的历史了。公元前 3 世纪,古希腊数学家欧几里得写出了举世闻名的巨著《原本》,在这本书中,他挑选了一些基本定义和基本事实作为证实其他命题的出发点,推导出 400 多条定理,《原本》是人类智慧的伟大成就之一,它对科学和人类文化和发展产生了深远的影响。情景创设情景创设徐光启于公元 1603 年在南京与利玛窦结识。公元 1604 年,他到翰林院做官后,就专门拜利玛窦为师,跟他学习西洋的天文历法、几何数学、武器制造等知识。 徐光启对数学非常有兴趣。他认为数学原则可以应用于各种实验科学,对于解决天文历法、测量建筑、武器制造等等都是有用的,好多学问都离不开数学。 一天,利玛窦跟徐光启谈起一本古老的西方数学名著《几何》,是古希腊数学家欧几里得写的。徐光启听得津津有味,觉得是本好书。于是,他与利玛窦商定,两人共同把此书翻译成中文,介绍给中国的读者。 从此,徐光启每天从翰林院下班,就来到利玛窦的住宅,利玛窦口述,徐光启笔写,翻译起《欧几里得原本》来。他们花了一年多时间,经过再三修改,才完成全部译稿,并定名为《几何原本》。全书共有六卷。现在数学中一些通用的术语、概念,如“几何”、“三角”、“直角”、“锐角”、“正弦”、“余弦”等等,都是由这部翻译书首先使用而流传下来的。情景创设下列语句是命题吗 ?过点 P 作直线 AB 的垂线 .同角的补角相等 .对顶角相等 .内错角相等 .内错角相等 , 两直线平行 .是真命题吗 ?复习回顾你能用推理的方法证实同角的补角相等吗 ?123互助讨论同位角相等 , 两直线平行 .两直线平行 , 同位角相等 .两边和它们夹角对应相等的两个三角形全等 .两角和它们的夹边对应相等的两个三角形全等 .三边对应相等的两个三角形全等 .原本基本事实证明 : 对顶角相等 .例题精讲证明 : 对顶角角相等 .123abo例题精讲已知 : 直线 a 、 b 被直线 c 所 截, 1 = 2求证: a b3证明 : 内错角相等 , 两直线平行 .21abc例题精讲证明 : 同旁内角互补 , 两直线平行 .例题精讲直线 a 、 b 被直线 c 所截,(1) 如果 2 = 8 ,你能得到什么结论?证明你的结论 .(2) 在 1 、 2 、 3 8 这八个角中, 由哪些条件可以证明a ‖ b c7 ...