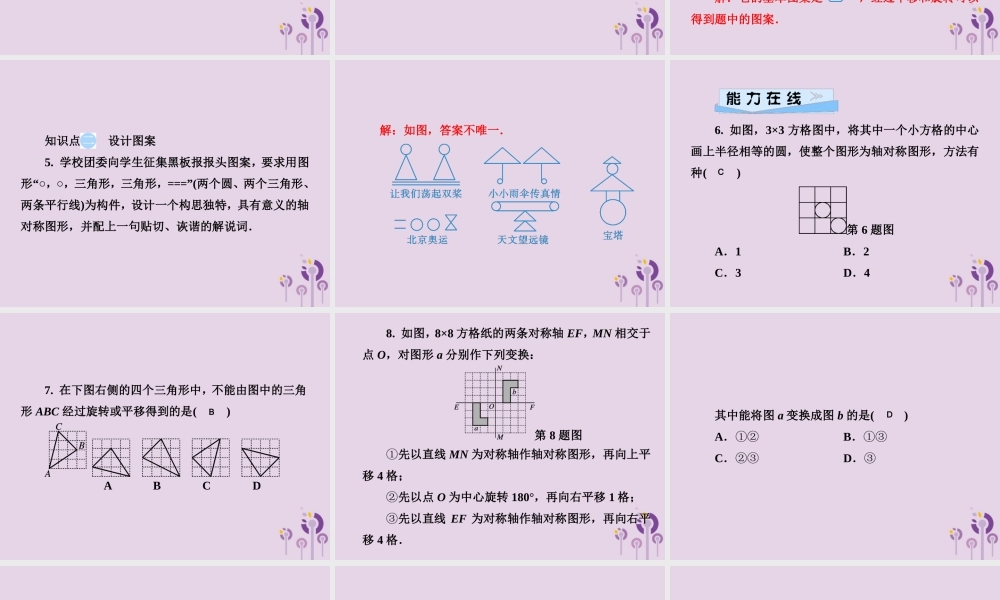
第五章 轴对称与旋转5.3 图形变换的简单应用 1. 平移和旋转都是图形运动的一种形式,在数学中被称为图形的变换.两种变换的特征是:图形经变换后,__________________. 2. 平移主要是距离的变化,旋转主要是角度的变化. 不改变其形状和大小 知识点 分析图案 1. 下列各网格中的图形是用其图形中的一部分平移得到的是( ) A B C D C 2. 如图①,三角形 ABC 和三角形 ADE 都是等腰直角三角形,∠ACB 和∠ADE 都是直角,点 C 在 AE 上,三角形 ABC 绕着 A 点经过逆时针旋转后能够与三角形ADE 重合得到图①,再将图①作为“基本图形”绕着 A 点经过逆时针连续旋转得到图.② 两次旋转的角度分别是( ) 第 2 题图 A A.45°,90° B.90°,45° C.60°,30° D.30°,60° 3. (2018·贺州)如图,将直角三角形 ABC 绕直角顶点C 顺时针旋转 90°,得到三角形 A′B′C,连接 BB′,若∠A′B′B=20°,则∠A 的度数是______. 第 3 题图 65° 4. 观察这个图案,你能说说它的“基本图案”是什么吗?这个图案又是怎样形成的呢? 解:它的基本图案是,经过平移和旋转可以得到题中的图案. 知识点 设计图案 5. 学校团委向学生征集黑板报报头图案,要求用图形“○,○,三角形,三角形,===”(两个圆、两个三角形、两条平行线)为构件,设计一个构思独特,具有意义的轴对称图形,并配上一句贴切、诙谐的解说词. 解:如图,答案不唯一. 6. 如图,3×3 方格图中,将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,方法有种( ) 第 6 题图 A.1 B.2 C.3 D.4 C 7. 在下图右侧的四个三角形中,不能由图中的三角形 ABC 经过旋转或平移得到的是( ) A B C D B 8. 如图,8×8 方格纸的两条对称轴 EF,MN 相交于点 O,对图形 a 分别作下列变换: 第 8 题图 ①先以直线 MN 为对称轴作轴对称图形,再向上平移 4 格; ②先以点 O 为中心旋转 180°,再向右平移 1 格; ③先以直线 EF 为对称轴作轴对称图形,再向右平移 4 格. 其中能将图 a 变换成图 b 的是( ) A.①② B.①③ C.②③ D.③ D 9. 如图所示的图案由三个叶片组成,绕点 O 旋转120°后可以和自身重合.若每个叶片的面积为 4 cm2,∠AOB 为 120°,则图中阴影部分的面积之和为__cm2. 第 9 题图 4 10. 如图,这个五角星可以由一个基本图形...