九年级数学下册 实际问题与二次函数3精品课件 人教新课标版 课件VIP免费

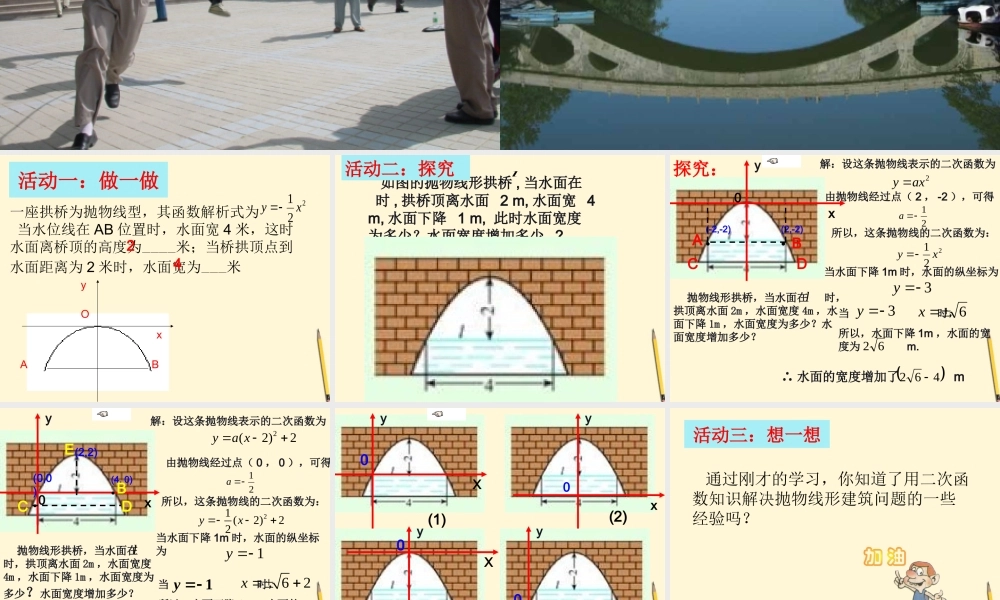
活动一：做一做 一座拱桥为抛物线型，其函数解析式为 当水位线在 AB 位置时，水面宽 4 米，这时水面离桥顶的高度为————米；当桥拱顶点到水面距离为 2 米时，水面宽为———米221 xyxyABO24 如图的抛物线形拱桥 , 当水面在 时 , 拱桥顶离水面 2 m, 水面宽 4 m, 水面下降 1 m, 此时水面宽度为多少？水面宽度增加多少 ?l活动二：探究 抛物线形拱桥，当水面在 时，拱顶离水面 2m ，水面宽度 4m ，水面下降 1m ，水面宽度为多少？水面宽度增加多少？lxy0(2,-2)●(-2,-2)●当 时，所以，水面下降 1m ，水面的宽度为 m.3y6x62462∴ 水面的宽度增加了 m探究：2axy 解：设这条抛物线表示的二次函数为21a由抛物线经过点（ 2 ， -2 ），可得221 xy所以，这条抛物线的二次函数为：3y当水面下降 1m 时，水面的纵坐标为ABCD 抛物线形拱桥，当水面在 时，拱顶离水面 2m ，水面宽度4m ，水面下降 1m ，水面宽度为多少？水面宽度增加多少？lxy0(4, 0)●(0,0)●462∴ 水面的宽度增加了 m(2,2)2(2)2ya x解：设这条抛物线表示的二次函数为21a由抛物线经过点（ 0 ， 0 ），可得21 (2)22yx所以，这条抛物线的二次函数为：当 时，所以，水面下降 1m ，水面的宽度为 m.1y6262x 1y 当水面下降 1m 时，水面的纵坐标为CDBE X yxy0 0X y0X y0(1)(2)(3)(4) 活动三：想一想 通过刚才的学习，你知道了用二次函数知识解决抛物线形建筑问题的一些经验吗？ 建立适当的直角坐标系审题，弄清已知和未知合理的设出二次函数解析式 求出二次函数解析式 利用解析式求解得出实际问题的答案 有一抛物线型的立交桥拱，这个拱的最大高度为 16 米，跨度为 40 米，若跨度中心M 左，右 5 米处各垂直竖立一铁柱支撑拱顶，求铁柱有多高？活动四：练一练 利用二次函数知识解决实际问题的一般步利用二次函数知识解决实际问题的一般步骤：骤：1 . 1 . 审题审题 ,, 弄清已知和未知。弄清已知和未知。2 . 2 . 将实际问题转化为数学问题。建立适将实际问题转化为数学问题。建立适当的平面直角坐标系当的平面直角坐标系小结反思小结反思小结反思小结反思3 .3 . 根据题意找出点的坐标，求出抛物线 根据题意找出点的坐标，求出抛物线 解析式 解析式。。分析图象，解分析图象，解决实际问题。决实际问题。3 .3 . 根...