九年级数学下册 52(二次函数的图象和性质)二次函数yax h2k的图象课件 (新版)苏科版 课件VIP免费

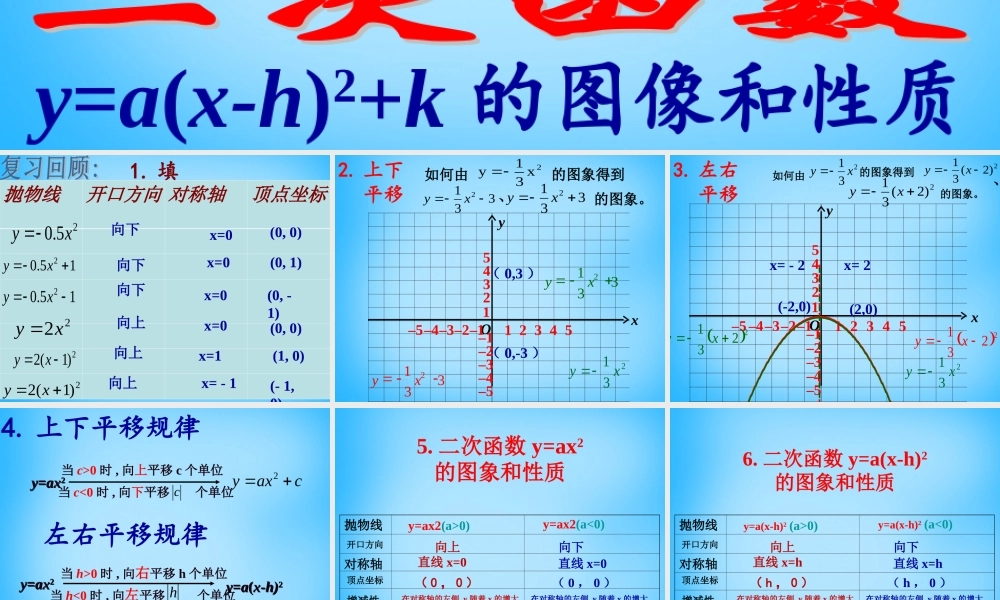
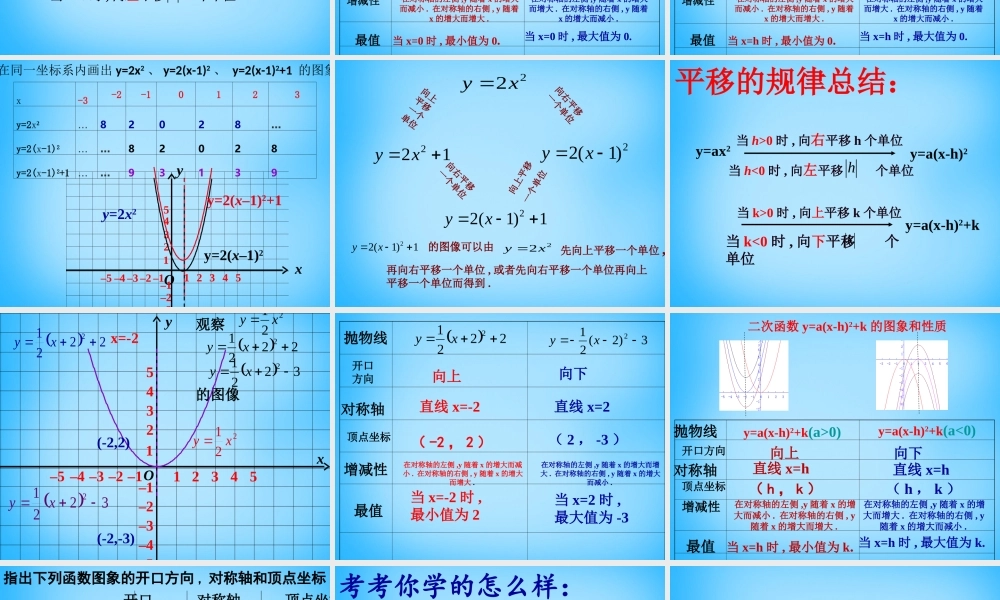
8642-2-4-6-10-5510xxyy111122223333444455556677-1-1-1-1-2-2-3-3-4-4-5-500-2-223xy y=a(x-h)2+k 的图像和性质1. 填表抛物线开口方向 对称轴顶点坐标 25.0 xy15.02 xy15.02 xy22xy 2)1(2 xy2)1(2xy(0, 0)(1, 0)(- 1, 0)(0, 0)(0, 1)(0, - 1)向下向下向下向上向上向上x=0x=0x=0x=0x=1x= - 1Oxy1 2 3 4 512345–5 –4 –3 –2 –1 –5 –4 –3 –2 –1 231 xy（ 0,3 ）（ 0,-3 ）如何由 2x31y的图象得到 3312 xy3312 xy的图象。2. 上下 平移、3312 xy3312 xyOxy1 2 3 4 512345–5 –4 –3 –2 –1 –5 –4 –3 –2 –1 231 xy2231xy2231xyx= - 2(-2,0)(2,0)x= 2如何由 231 xy的图象得到 2)2(31xy2)2(31xy的图象。、3. 左右 平移yy==axax22 当 h>0 时 , 向右平移 h 个单位当 h<0 时 , 向左平移 个单位yy==aa((x-h)x-h)22hyy==axax22当 c>0 时 , 向上平移 c 个单位当 c<0 时 , 向下平移 个单位caxy2c4. 上下平移规律左右平移规律5. 二次函数 y=ax2的图象和性质抛物线顶点坐标对称轴开口方向增减性最值y=ax2(a>0)y=ax2(a<0)（ 0 ， 0 ）（ 0 ， 0 ）直线 x=0直线 x=0向上向下当 x=0 时 , 最小值为 0.当 x=0 时 , 最大值为 0.在对称轴的左侧 ,y 随着 x 的增大而减小 . 在对称轴的右侧 , y 随着x 的增大而增大 . 在对称轴的左侧 ,y 随着 x 的增大而增大 . 在对称轴的右侧 , y 随着x 的增大而减小 . 6. 二次函数 y=a(x-h)2的图象和性质抛物线顶点坐标对称轴开口方向增减性最值y=a(x-h)2 (a>0)y=a(x-h)2 (a<0)（ h ， 0 ）（ h ， 0 ）直线 x=h直线 x=h向上向下当 x=h 时 , 最小值为 0.当 x=h 时 , 最大值为 0.在对称轴的左侧 ,y 随着 x 的增大而减小 . 在对称轴的右侧 , y 随着x 的增大而增大 . 在对称轴的左侧 ,y 随着 x 的增大而增大 . 在对称轴的右侧 , y 随着x 的增大而减小 . Oxy1 2 3 4 512345–5 –4 –3 –2 –1 –3 –2 –1 y=2x2y=2(x–1)2y=2(x–1)2+1x-3-2-10123y=2x2…82028…y=2(x-1)2……82028y=2(x-1)2+1……93139在同一坐标系内画出 y=2x2 、 y=2(x-1)2 、 y=2(x-1)2+1 的图象22xy 122  xy1)1(...